nextnano3 - Tutorial
next generation 3D nano device simulator
1D Tutorial
Solution of the Poisson equation for different charge density profiles
Author:
Stefan Birner
If you want to obtain the input files that are used within this tutorial, please
check if you can find them in the installation directory.
If you cannot find them, please submit a
Support Ticket.
1) -> 1D_Poisson_dipole.in / *_nnp.in - input file for the nextnano3 and nextnano++ software
(1D simulation)
2) -> 1D_Poisson_linear.in
3) -> 1D_Poisson_delta.in
1) Dipole: Constant charge density profile of positive and
negative charge
2) Linear charge density profile of positive and negative
charge
3) Delta-function like charge density profile of positive and
negative charges
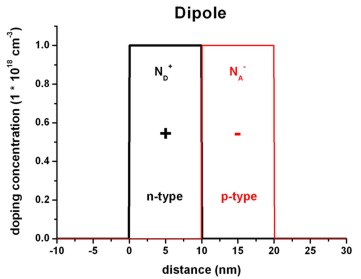
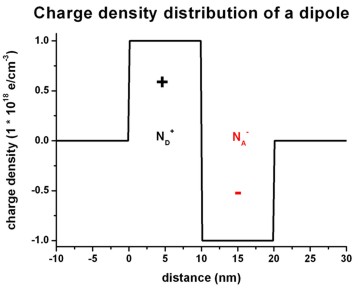
The following figures show a dipole charge density distribution where
- the left region carries a constant positive
charge density (resulting from ionized donors ND+)
and
- the right region carries a constant negative charge density
(resulting from ionized acceptors NA-).
Left figure: 1Ddoping_concentration.dat
Right figure: densities/density1Dspace_charge.dat
We have to solve the Poisson equation: d2phi / dx2
= - rho / (epsilon epsilon0)
The following figures shows the corresponding electric field distribution (left)
and the electrostatic potential (right).
Left figure: band_structure/electric_field1D.dat
Right figure: band_structure/potential1D.dat
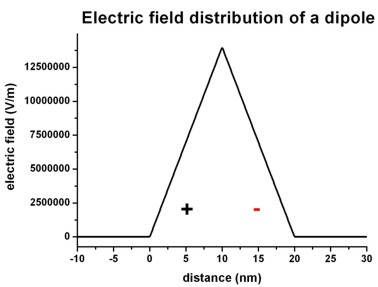
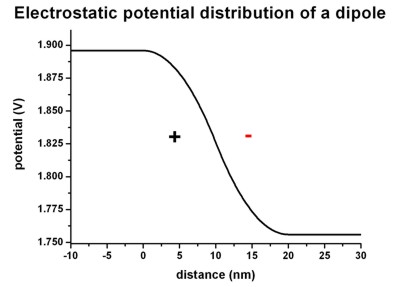
The electric field is given by E(x) = - dphi / dx and
has a linear dependence (~ -x) because the electrostatic potential
has a quadratic dependence (~ x2).
The maximum value of the electric field is given by:
Emax = rho / (epsilon epsilon0) * x0 = e * 1*1018
cm-3 / ( 12.93 * 8.8542*10-12 As/Vm
) * 10 nm =
= 1.3995*107 V/m = 139.95
kV/cm
The drop of the electrostatic potential between 0 nm and 20 nm is simply given
by the area that is below the graph of the electric field:
Delta phi = 1/2 Emax * 20 nm =
139.95 mV
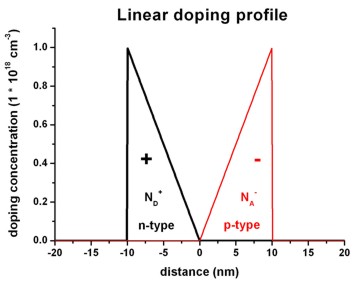
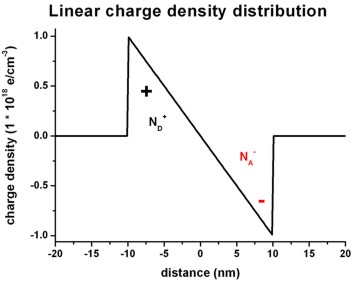
The following figures show a linearly varying charge density distribution
where
- the left region carries a linearly decreasing
positive charge density (resulting from ionized donors
ND+) and
- the right region carries a linearly increasing negative
charge density (resulting from ionized acceptors NA-).
Left figure: 1Ddoping_concentration.dat
Right figure: densities/density1Dspace_charge.dat
The following figures shows the corresponding electric field distribution (left)
and the electrostatic potential (right).
Left figure: band_structure/electric_field1D.dat
Right figure: band_structure/potential1D.dat
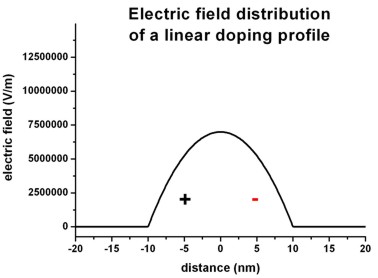
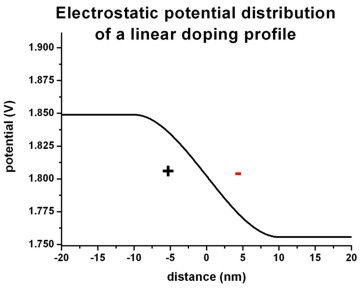
The electric field shows a quadratic dependence (~ -x2)
whereas the electrostatic potential shows a cubic dependence (~ x3).
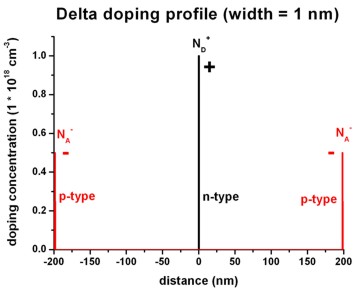
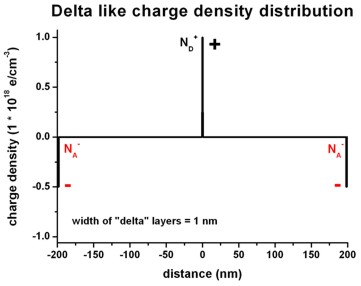
The following figures show a delta-function like charge density distribution
where
- in the middle of the
structure there is a constant positive charge density of width
1 nm (resulting from ionized
donors ND+) and
- at the boundaries of the structure there are constant negative
charge densities of width 1 nm each (resulting from ionized acceptors NA-).
Left figure: 1Ddoping_concentration.dat
Right figure: densities/density1Dspace_charge.dat
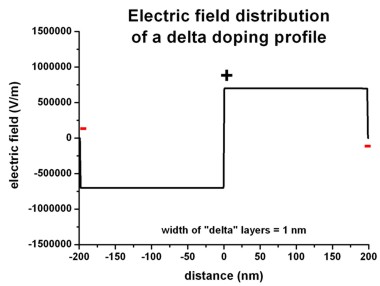
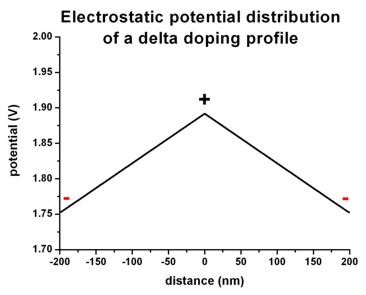
The following figures shows the corresponding electric field distribution (left)
and the electrostatic potential (right).
Left figure: band_structure/electric_field1D.dat
Right figure: band_structure/potential1D.dat
|