This is the old documentation.
Here's the link to the new documentation.
cbr{}
Specifications that define CBR (contact block reduction
method) calculation, i.e. ballistic current calculations.
Efficient method for the calculation of ballistic quantum transport
D. Mamaluy, M. Sabathil, and P. Vogl
J. Appl. Phys. 93, 4628 (2003)
Ballistic Quantum Transport using the Contact Block Reduction (CBR) Method - An introduction
S. Birner, C. Schindler, P. Greck, M. Sabathil, P. Vogl
Journal of Computational Electronics (2009)
At a glance: CBR current calculation
- full 1D, 2D and 3D calculation of quantum mechanical ballistic
transmission probabilities for open systems with scattering boundary
conditions
- Contact Block Reduction method:
- only
incomplete set of quantum states needed (~ 100)
- reduction of matrix
sizes from O(N³) to O(N²)
- ballistic current according to Landauer-Büttiker formalism
The CBR method is an efficient method that uses a
limited set of eigenstates of the decoupled device and a few propagating lead
modes to calculate the retarded Green's function of the device coupled to
external contacts. From this Green's function, the density and the current is
obtained in the ballistic limit using Landauer's formula with fixed Fermi levels
for the leads.
It is important to note that the efficiency of
the calculation and also the convergence of the results are strongly dependent
on the cutoff energies for the eigenstates and modes. Thus it is important to
check during the calculation if the specified number of states and modes is
sufficient for the applied voltages. To summarize, the code may do its job very
efficiently but is far away from being a black box tool.
cbr{
name = "qr"
# refers to quantum region to which CBR method will be applied
(d-dimensional)
lead{ name =
"lead_1" }
#
rel_min_energy = -0.01
# Lower boundary for transmission energy interval relative to lowest
eigenvalue
(default is: -0.01)
rel_max_energy = 0.3
# Upper boundary for transmission energy interval relative to highest
eigenvalue
(default is: 1.01)
abs_min_energy = 2.5 # Lower boundary for transmission energy interval
on an absolute energy scale
(default is: 0.0)
abs_max_energy = 2.6
# Upper boundary for transmission energy interval on an absolute energy
scale
(default is: 0.0)
# Specify
either rel_min_energy
and rel_max_energy
or abs_min_energy
and abs_max_energy.
delta_energy = 1e-6
# 1e-4 [eV])
ildos =
yes
# outputs integrated local density of states (default is: no)
options =
[1, 0, 0] #
=
[..., ..., ..., ...]
# 11 values are needed for two particle model
# numStates2_ = (int)options_[0];
# const double epsRel = options_[1];
# const DVector3
r1(options_[2]*uNanometer,options_[3]*uNanometer,options_[4]*uNanometer);
# const DVector3
r2(options_[5]*uNanometer,options_[6]*uNanometer,options_[7]*uNanometer);
# const double delta = options_[8]*uEVolt; // splitting
# const double z = options_[9]*uEVolt; // tunneling
#
# // [prefactor] = Q^2/[cEps0], [cEps0] = Q/L*V => [prefactor] = Q L V = eV L
#
# const double prefactor = options_[10] * sqr(cEcharge)/(4*Pi*epsRel*cEps0);
}
Example
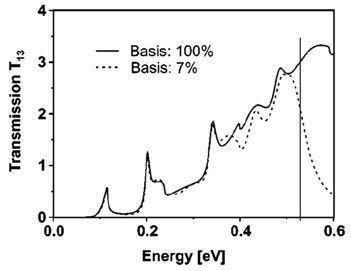
The following figure shows the calculated transmission from
lead 1 to lead 3 as a function of energy T13(E).
Full line: All eigenfunctions of the decoupled
device are taken into account.
Dashed line: Only the lowest 7% of the eigenfunctions are included.
Here, Neumann boundary conditions are used for the propagation direction.
The vertical line indicates the cutoff energy, i.e. the highest eigenvalue
that is taken into account.
Additional notes
Special boundary conditions for CBR method
-> Along propagation direction Neumann
boundary conditions are applied to the Schrödinger equation.
->
Perpendicular to the propagation direction Dirichlet boundary conditions
are applied to the Schrödinger equation.
Note: Physically speaking, the lead quantum cluster must be a two-dimensional
surface in a 3D simulation, a one-dimensional line in a 2D simulation and a
zero-dimensional point in a 1D simulation.
|