|
| |
nextnano3 - Tutorial
next generation 3D nano device simulator
1D Tutorial
Strain and displacement tensors along different growth directions
Author:
Stefan Birner
If you want to obtain the input files that are used within this tutorial, please
check if you can find them in the installation directory.
If you cannot find them, please submit a
Support Ticket.
-> 1DstrainN11.in / *_nnp.in -
input file for the nextnano3 and nextnano++ software
-> 2DstrainN11.in / *_nnp.in -
-> 3DstrainN11.in / *_nnp.in -
AlAs/InAs/AlAs structure on InP
- This input file simulates a InP/InAs/AlAs structure grown
pseudomorphically on InP:
1DstrainN11.in
The structure is grown pseudomorphically on InP, i.e. the InAs is
compressively strained, the AlAs is tensilely strained. The growth direction [N11]
is along x, the interfaces are in the (y,z) plane.
- This tutorial examines the strain tensors in the
crystal and
simulation coordinate system as well as the corresponding displacement
tensors.
The following parameters are used:
| |
InP (substrate) |
InAs |
AlAs |
| Lattice
constant a (nm) |
0.58697 |
0.60583 |
0.56611 |
| Elastic
constant c11 (GPa) |
101.1 |
83.29 |
125.0 |
| Elastic
constant c12 (GPa) |
56.1 |
45.26 |
53.4 |
| Elastic
constant c44 (GPa) |
45.6 |
39.59 |
54.20 |
- [100] growth direction
(y direction along [010])
$domain-coordinates
...
hkl-x-direction-zb = 1 0 0 ! Miller indices
of x coordinate axis [1 0 0]
hkl-y-direction-zb = 0 1 0 ! Miller indices
of y coordinate axis [0 1 0]
growth-coordinate-axis = 1 0 0
...
The strain tensors in the
crystal and
simulation system are identical. Off-diagonal strain components eij
are zero. The hydrostatic strain is defined as the trace of the strain tensor
(ehydro=exx+eyy+ezz). It is useful
to talk about parallel strain (e||=eyy=ezz)
and perpendicular (e_|_=exx) strain with respect to the
interface coordinate system.
Biaxial strain (in plane of interface):
InAs: e|| = eyy = ezz
= ( asubstrate - alayer ) / alayer = -0.0311308 (3.1 % lattice mismatch)
Uniaxial strain (perpendicular to interface):
InAs: e_|_ = exx = - D100 e||
= - 2 (c12/c11) e||
= 0.0338332
For [100] growth direction the strain tensors and the displacement tensors
coincide.
|
[100] |
exx=e_|_ |
eyy=ezz=e|| |
ehydro |
|
InAs |
0.338332E-001 |
-0.311308E-001 |
-0.284285E-001 |
|
AlAs |
-0.314829E-001 |
0.368480E-001 |
0.422130E-001 |
- [011] growth direction
(y direction along [01-1])
$domain-coordinates
...
hkl-x-direction-zb = 0 1 1 ! Miller indices
of x coordinate axis [1 0 0]
hkl-y-direction-zb = 0 1 -1 ! Miller indices of y
coordinate axis [0 1 0]
growth-coordinate-axis = 1 0 0
...
The strain tensors in the
crystal and
simulation system are not identical any more. Off-diagonal strain
components eij are zero apart from eyzcr. The
hydrostatic strain is independent of coordinate system.
Biaxial strain (in plane of interface):
InAs: e||=eyysim = ezzsim
= ( asubstrate - alayer ) / alayer = -0.0311308 (same
as for [100])
Uniaxial strain (perpendicular to interface):
InAs: e_|_ =exxsim
= - D011e|| = - (c11+3c12-2c44) / (c11+c12+2c44) e||
= 0.0209642
Crystal system: InAs: eyycr = ezzcr
= - ??? e||
= -0.00508332
InAs: eyzcr = - (c11+2c12)
/ (c11+c12+2c44) e||
= 0.0260475
For [011] growth direction the strain tensors and the displacement tensors
coincide.
Here it is interesting to note that exxcr = e||.
|
[011] |
exxsim=e_|_ |
eyysim=ezzsim=e|| |
ehydro |
|
InAs |
0.209642E-001 |
-0.311308E-001 |
-0.412975E-001 |
|
AlAs |
-0.227152E-001 |
0.368480E-001 |
0.509807E-001 |
|
[011] |
exxcr |
eyycr=ezzcr |
eyzcr |
|
InAs |
-0.311308E-001 |
-0.508332E-002 |
0.260475E-001 |
|
AlAs |
0.368480E-001 |
0.706638E-002 |
-0.297816E-001 |
- [111] growth direction
(y direction along [01-1])
$domain-coordinates
...
hkl-x-direction-zb = 1 1 1 ! Miller indices
of x coordinate axis [1 0 0]
hkl-y-direction-zb = 0 1 -1 ! Miller indices of y
coordinate axis [0 1 0]
growth-coordinate-axis = 1 0 0
...
The strain tensors in the
crystal and
simulation system are not identical. Off-diagonal strain components eij
are still zero in the simulation system but not in the crystal system.
Simulation system:
Biaxial strain (in plane of interface):
InAs: e||=eyysim = ezzsim
= ( asubstrate - alayer ) / alayer = -0.0311308 (same
as for [100])
Uniaxial strain (perpendicular to interface):
InAs: e_|_ =exxsim
= - D111e|| = - 2(c11+2c12-2c44)
/ (c11+2c12+4c44) e||
= 0.0177374
Crystal system: InAs: exxcr = eyycr
= ezzcr = - (-4c44)
/ (c11+2c12+4c44) e||
= -0.0148414
InAs: exycr = exzcr
= eyzcr = - (c11+2c12)
/ (c11+2c12+4c44) e||
= 0.0162894
For [111] growth direction the strain tensors and the displacement tensors
coincide.
|
[111] |
exxsim=e_|_ |
eyysim=ezzsim=e|| |
ehydro |
|
InAs |
0.177374E-001 |
-0.311308E-001 |
-0.445243E-001 |
|
AlAs |
-0.202721E-001 |
0.368480E-001 |
0.534238E-001 |
|
[111] |
exxcr=eyycr=ezzcr |
exycr=exzcr=eyzcr |
|
|
InAs |
-0.148414E-001 |
0.162894E-001 |
|
|
AlAs |
0.178079E-001 |
-0.190400E-001 |
|
- [211] growth direction
(y direction along [01-1])
$domain-coordinates
...
hkl-x-direction-zb = 2 1 1 ! Miller indices
of x coordinate axis [1 0 0]
hkl-y-direction-zb = 0 1 -1 ! Miller indices of y
coordinate axis [0 1 0]
growth-coordinate-axis = 1 0 0
...
Off-diagonal strain components eij are not zero any more in the
simulation system. For [211] growth direction the strain tensors and the
displacement tensors do not coincide any more because the displacement tensors
are not symmetric any more. The diagonal entries still coincide eii=uii.
Biaxial strain (in plane of interface):
InAs: e||=eyysim = ezzsim
= ( asubstrate - alayer ) / alayer = -0.0311308 (same
as for [100])
Uniaxial strain (perpendicular to interface):
InAs: e_|_ =exxsim
= - D211e|| = - (D211=???) e||
= 0.0228540
|
[211] |
exxsim=e_|_ |
eyysim=ezzsim=e|| |
exzsim |
ehydro |
|
uzxsim=duz/dx |
uxzsim=dux/dz |
|
InAs |
0.228540E-001 |
-0.311308E-001 |
-0.101187E-001 |
-0.394077E-001 |
|
-0.202373E-001 = 2exzsim |
0 |
|
AlAs |
-0.234699E-001 |
0.368480E-001 |
0.623832E-002 |
0.502260E-001 |
|
0.124766E-001
= 2exzsim |
0 |
|
[211] |
exxcrr |
eyycr=ezzcr |
exycr=exzcr |
eyzcr |
uxycr=uxzcr |
uyxcr=uzxcr |
uyzcr=uzycr |
|
InAs |
0.143990E-001 |
-0.269034E-001 |
0.156100E-001 |
0.422749E-002 |
0.227649E-001 |
0.845498E-002 |
0.422749E-002 = eyzcr |
|
AlAs |
-0.924548E-002 |
0.297358E-001 |
-0.186356E-001 |
-0.711220E-002 |
-0.230467E-001 |
-0.142244E-001 |
-0.711220E-002
= eyzcr |
One can see that the displacement tensor for the simulation system is
rather nice as the following off-diagonal components are zero:
- uxysim, uxzsim, uyzsim
are always zero for 1D structures grown along the x axis of the simulation
system.
- uyxsim, uzysim are zero in
this particular example.
Here one should recall the definiton of the strain tensor: eij =
1/2 (uij + uji) = 1/2 (dui/dj + duj/di)
The strain tensor is thus always symmetric but the displacement tensor only
for growth directions along [001], [011], [111]. In fact, for these three
directions it is also diagonal in the simulation coordinate system. In this
particular example, uxycr
is not equal to uyxcr.
- [311] growth direction
(y direction along [01-1])
$domain-coordinates
...
hkl-x-direction-zb = 3 1 1 ! Miller indices
of x coordinate axis [1 0 0]
hkl-y-direction-zb = 0 1 -1 ! Miller indices of y
coordinate axis [0 1 0]
growth-coordinate-axis = 1 0 0
...
See comments for [211] growth direction
Biaxial strain (in plane of interface):
InAs: e||=eyysim = ezzsim
= ( asubstrate - alayer ) / alayer = -0.0311308 (same
as for [100])
Uniaxial strain (perpendicular to interface):
InAs: e_|_ =exxsim
= - D311e|| = - (D311=???) e||
= 0.0277907
|
[311] |
exxsim=e_|_ |
eyysim=ezzsim=e|| |
exzsim |
ehydro |
|
uzxsim=duz/dx |
uxzsim=dux/dz |
|
InAs |
0.277907E-001 |
-0.311308E-001 |
-0.111833E-001 |
-0.344710E-001 |
|
-0.223666E-001 = 2exzsim |
0 |
|
AlAs |
-0.267795E-001 |
0.368480E-001 |
0.714093E-002 |
0.469164E-001 |
|
0.142819E-001
= 2exzsim |
0 |
|
[311] |
exxcrr |
eyycr=ezzcr |
exycr=exzcr |
eyzcr |
uxycr=uxzcr |
uyxcr=uzxcr |
uyzcr=uzycr |
|
InAs |
0.257044E-001 |
-0.300877E-001 |
0.110373E-001 |
0.104316E-002 |
0.189451E-001 |
0.312949E-002 |
0.104316E-002 = eyzcr |
|
AlAs |
-0.207193E-001 |
0.338179E-001 |
-0.141397E-001 |
-0.303010E-002 |
-0.191891E-001 |
-0.909030E-002 |
-0.303010E-002
= eyzcr |
- [411] growth direction
(y direction along [01-1])
$domain-coordinates
...
hkl-x-direction-zb = 4 1 1 ! Miller indices
of x coordinate axis [1 0 0]
hkl-y-direction-zb = 0 1 -1 ! Miller indices of y
coordinate axis [0 1 0]
growth-coordinate-axis = 1 0 0
...
See comments for [211] growth direction
Biaxial strain (in plane of interface):
InAs: e||=eyysim = ezzsim
= ( asubstrate - alayer ) / alayer = -0.0311308 (same
as for [100])
Uniaxial strain (perpendicular to interface):
InAs: e_|_ =exxsim
= - D411e|| = - (D411=???) e||
= 0.0302133
|
[411] |
exxsim=e_|_ |
eyysim=ezzsim=e|| |
exzsim |
ehydro |
|
uzxsim=duz/dx |
uxzsim=dux/dz |
|
InAs |
0.302133E-001 |
-0.311308E-001 |
-0.986895E-002 |
-0.320484E-001 |
|
-0.197379E-001 = 2exzsim |
0 |
|
AlAs |
-0.285575E-001 |
0.368480E-001 |
0.646539E-002 |
0.451384E-001 |
|
0.129308E-001
= 2exzsim |
0 |
|
[411] |
exxcrr |
eyycr=ezzcr |
exycr=exzcr |
eyzcr |
uxycr=uxzcr |
uyxcr=uzxcr |
uyzcr=uzycr |
|
InAs |
0.296003E-001 |
-0.308243E-001 |
0.820438E-002 |
0.306496E-003 |
0.151828E-001 |
0.122598E-002 |
0.306496E-003 = eyzcr |
|
AlAs |
-0.253540E-001 |
0.352462E-001 |
-0.109788E-001 |
-0.160176E-002 |
-0.155505E-001 |
-0.640704E-002 |
-0.160176E-002
= eyzcr |
- [511] growth direction
(y direction along [01-1])
$domain-coordinates
...
hkl-x-direction-zb = 5 1 1 ! Miller indices
of x coordinate axis [1 0 0]
hkl-y-direction-zb = 0 1 -1 ! Miller indices of y
coordinate axis [0 1 0]
growth-coordinate-axis = 1 0 0
...
See comments for [211] growth direction
Biaxial strain (in plane of interface):
InAs: e||=eyysim = ezzsim
= ( asubstrate - alayer ) / alayer = -0.0311308 (same
as for [100])
Uniaxial strain (perpendicular to interface):
InAs: e_|_ =exxsim
= - D511e|| = - (D511=???) e||
= 0.0314570
|
[511] |
exxsim=e_|_ |
eyysim=ezzsim=e|| |
exzsim |
ehydro |
|
uzxsim=duz/dx |
uxzsim=dux/dz |
|
InAs |
0.314570E-001 |
-0.311308E-001 |
-0.847870E-002 |
-0.308047E-001 |
|
-0.169574E-001 = 2exzsim |
0 |
|
AlAs |
-0.295219E-001 |
0.368480E-001 |
0.563906E-002 |
0.441740E-001 |
|
0.112781E-001
= 2exzsim |
0 |
|
[511] |
exxcrr |
eyycr=ezzcr |
exycr=exzcr |
eyzcr |
uxycr=uxzcr |
uyxcr=uzxcr |
uyzcr=uzycr |
|
InAs |
0.312618E-001 |
-0.310333E-001 |
0.648318E-002 |
0.975671E-004 |
0.124785E-001 |
0.487835E-003 |
0.975671E-004 = eyzcr |
|
AlAs |
-0.275593E-001 |
0.358666E-001 |
-0.889403E-002 |
-0.981324E-003 |
-0.128815E-001 |
-0.490662E-002 |
-0.981324E-003
= eyzcr |
- [321] growth direction
(y direction along [-111])
$domain-coordinates
...
hkl-x-direction-zb = 3 2 1 ! Miller indices
of x coordinate axis [1 0 0]
hkl-y-direction-zb = -1 1 1 ! Miller indices of y
coordinate axis [0 1 0]
growth-coordinate-axis = 1 0 0
...
Biaxial strain (in plane of interface):
InAs: e||=eyysim
= ezzsim = ( asubstrate - alayer ) / alayer = -0.0311308 (same
as for [100])
Uniaxial strain (perpendicular to interface):
InAs: e_|_
=exxsim = - D321e||
= - (D321=???) e|| = 0.0223345
|
[321] |
exxsim=e_|_ |
eyysim=ezzsim=e|| |
exysim |
exzsim |
ehydro |
uyxsim=duy/dx |
uzxsim=duz/dx |
uxysim=uxzsim |
|
InAs |
0.223345E-001 |
-0.311308E-001 |
-0.871721E-002 |
0.139475E-002 |
-0.399271E-001 |
-0.174344E-001 = 2exysim |
0.278950E-002 = 2exzsim |
0 |
|
AlAs |
-0.232538E-001 |
0.368480E-001 |
0.528954E-002 |
-0.515392E-003 |
0.504421E-001 |
0.105791E-001
= 2exysim |
-0.103078E-002
= 2exzsim |
0 |
|
[321] |
exxcrr |
eyycr |
ezzcr |
exycr |
exzcr |
eyzcr |
|
InAs |
0.116554E-001 |
-0.221557E-001 |
-0.294269E-001 |
0.209935E-001 |
0.968697E-002 |
0.394774E-002 |
|
AlAs |
-0.681357E-002 |
0.232809E-001 |
0.339748E-001 |
-0.247292E-001 |
-0.115866E-001 |
-0.626491E-002 |
|
[321] |
uxycr |
uyxcr |
uxzcr |
uzxcr |
uyzcr |
uzycr |
|
InAs |
0.285242E-001 |
0.134627E-001 |
0.142621E-001 |
0.511185E-002 |
0.448757E-002 |
0.340790E-002 |
|
AlAs |
-0.291077E-001 |
-0.203506E-001 |
-0.145538E-001 |
-0.861942E-002 |
-0.678354E-002 |
-0.574628E-002 |
- Simulation system
Now we plot the above results for [N11] growth directions. Note that [100] is
identical to ["infinity"11] growth direction. All plotted quantities are given
in the simulation system.
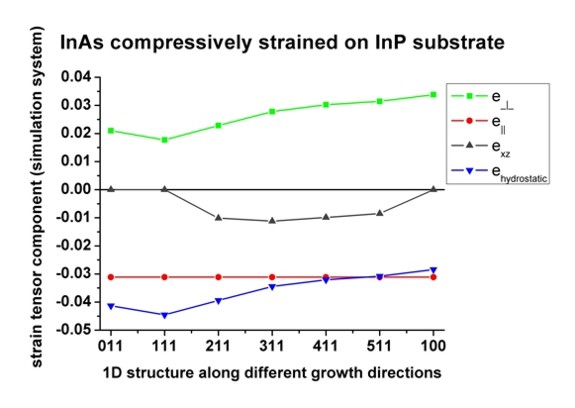
For [011], [111] and [100], the off-diagonal strain tensor component exzsim
is zero. For the "high symmetry growth
directions" the strain and displacement tensors are diagonal. (But this
does not necessarily mean that shear strain is absent. Shear strain is only
absent if the strain tensor is diagonal in the crystal system, i.e. only for
[100] growth direction.)
The hydrostatic strain ehy=Tr(eij) is always negative
because we have a volume reduction (compressive strain). It has the largest
value in magnitude for [111] and the smallest in magnitude for [100]. It shows
exactly the same behaviour as the curve for e_|_sim,
i.e. e_|_sim is a measure for the volume deformation in
the growth direction.
The strain in the plane of interface e||sim is constant
for all growth directions.
Note that the highest value for offdiagonal strain exz occurs for
[311] growth direction (highest shear strain of any orientation).
- Crystal system
Now we plot the above results for [N11] growth directions. Note that [100] is
identical to ["infinity"11] growth direction. All plotted quantities are given
in the crystal system.
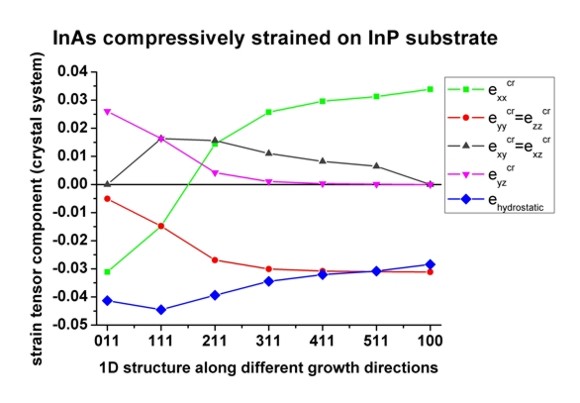
The hydrostatic strain ehy=Tr(eij) is identical to the
plot of the simulation system. (The trace of a matrix is independent of
coordinate system.) It is always negative because we have a volume reduction
(compressive strain). It has the largest value in magnitude for [111] and the
smallest in magnitude for [100].
For [111] growth direction, exxcr=eyycr=ezzcr
and exycr=exzcr=eyzcr.
All off-diagonal components are zero only for [100] growth direction (no shear
strain). For all other orientations we have shear strain. Shear strain (with
respect to the crystal system) is responsible for piezoelectric effects.
The off-diagonal components exycr=exzcr
are zero for [011] growth direction but the off-diagonal component eyzcr
is not.
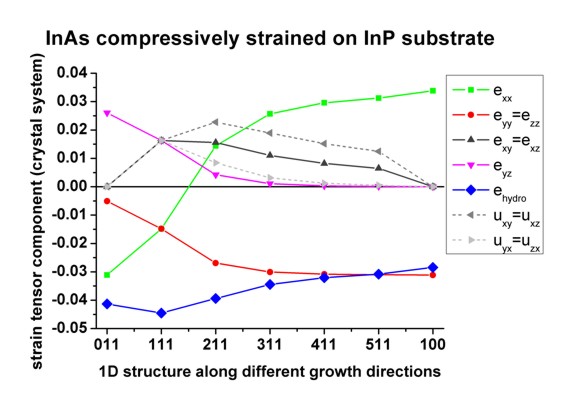
- Here the same picture is plotted again (crystal system) but this
time including the important components of the displacement tensor that are
responsible for the fact that the displacement tensor is not symmetric any
more for [211], [311], [411] and [511].
The strain tensor is defined as: eij = 1/2 (uij + uji)
= 1/2 (dui/dj + duj/di)
Thus:
| exycr
= 1/2 (uxycr+uyxcr). |
For the high symmetry growth direction [100], [011], [111] the displacement
tensor is symmetric because
- Strain has important effects:
- piezoelectric fields: See Tutorial on
piezoelectricity.
- shifts and splittings of conduction and valence bands:
See Tutorial on deformation potentials.
- strain changes the k.p Hamiltonian
- Strain can be used to tailor the electronic and optical properties of
heterostructures.
|