nextnano³ - Tutorial

next generation 3D nano device simulator

1D Tutorial

Strained AlAs QW - Crossover of ground states

Author: Stefan Birner

If you want to obtain the input files that are used within this tutorial, please check if you can find them in the installation directory.
If you cannot find them, please submit a Support Ticket.
-> 1DAlAs_QW_4nm_001.in
-> 1DAlAs_QW_8nm_001.in

-> 1DAlAs_QW_4nm_011.in
-> 1DAlAs_QW_8nm_011.in

-> 1DAlAs_QW_4nm_111.in
 

Strained AlAs QW along [001] - Crossover of ground states

-> 1DAlAs_QW_4nm_001.in
-> 1DAlAs_QW_8nm_001.in

Note: Please also have a look at this tutorial: AlAs QW crossover II

Conduction band edges and wave functions

The following figures show the conduction band edges at the X point for AlAs(001) QWs embedded within GaAs.
The square of the wave functions (psi²) - shifted by their energies - are shown for a 4 nm and 8 nm quantum well.
The X band in AlAs is split due to compressive strain with respect to the GaAs(001) substrate.
The X_xy band is two-fold degenerate (2 valleys at the X point). ==> m_DOS = (m_l m_t)^1/2
The X_z band is non-degenerate (1 valley at the X point).      ==> m_DOS = (m_t m_t)^1/2 = m_t
The X_z and X_xy valleys are separated due to strain by 21.6 meV.
The GaAs barriers are unstrained.
Only the two lowest confined wave functions are shown.

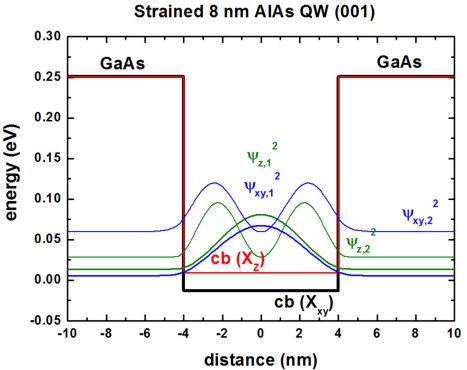
The longitudinal mass m_l is heavier in AlAs than the transverse masses m_t.
Consequently, one expects the ground state to be determined by the heavier longitudinal mass.
However, this is true only for QWs smaller than 6 nm.
For larger QW widths, the ground state is due to the other two valleys because here, the fact that these conduction band edges are the lowest in energy dominates.

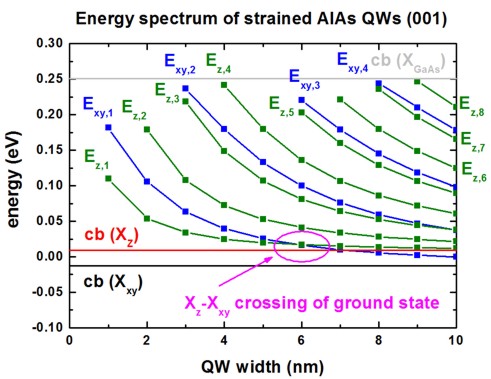
The following figure shows the energy spectrum of a strained AlAs(001) QW as a function of QW width.
Once can clearly see the crossing of the ground state at a QW width of ~6 nm.
For the 10 nm QW, 4 states of the X_xy valleys and 8 states of the X_z valleys are confined in the quantum well

Material parameters

• $numeric-control
 ...
 lattice-constants-temp-coeff-on = yes ! temperature dependent lattice constants
  
  $global-parameters
 lattice-temperature = 1d0 ! [K] 1 Kelvin
  
  T = 1 K, i.e. lattice constants are calculated for 1 K:
  ==> GaAs: 0.5642 nm
  ==> AlAs:  0.5652 nm
  
  These calculated values can be found in this file: lattice_constants1D.dat
 
• X band conduction band offset (CBO) GaAs/AlAs (unstrained): 0.251 eV = 3.441 - 3.190
  
  GaAs
 conduction-band-energies = ...  ...  3.441d0 ! [eV] Gamma, L, X

AlAs
 conduction-band-energies = ...  ...  3.190d0 ! [eV] Gamma, L, X

We shift both band edges by -3.190 so that the unstrained AlAs band edge is located at 0 eV.
 band-shift               = -3.190d0          ! [eV]
 
• GaAs
conduction-band-masses = ...                  ! [m0] Gamma cb1 - 1^st principal axis, 2^nd, 3^rd
                         ...                  ! [m0] L     cb2 - 1^st principal axis, 2^nd, 3^rd - ml mt mt
                         1.3d0  0.23d0 0.23d0 ! [m0] X     cb3 - 1^st principal axis, 2^nd, 3^rd - ml mt mt

AlAs
conduction-band-masses = ...                  ! [m0] Gamma cb1 - 1^st principal axis, 2^nd, 3^rd
                         ...                  ! [m0] L     cb2 - 1^st principal axis, 2^nd, 3^rd - ml mt mt
                         0.97d0 0.22d0 0.22d0 ! [m0] X     cb3 - 1^st principal axis, 2^nd, 3^rd - ml mt mt

  The mass tensor at the X conduction band edge is described with a longitudinal mass and two transverse masses (ellipsoidal mass tensor).

Strained AlAs QW along [011] - Crossover of ground states

-> 1DAlAs_QW_4nm_011.in
-> 1DAlAs_QW_8nm_011.in

Here, we grow the AlAs QW along the [011] direction.
This will affect the strain tensor, the shifts and splittings of the X conduction band edges and the orientation of the effective mass tensors of the different valleys.

 $domain-coordinates !
  ...
  growth-coordinate-axis = 0 0 1 !

  !++++++++++++++++++++ (011) surface +++++++++++++++++++++++++++++++++++++++++
   hkl-x-direction-zb = 1 0  0 ! along the [100]  direction in the crystal coordinate system
   hkl-y-direction-zb = 0 1 -1 ! along the [01-1] direction in the crystal coordinate system
  !hkl-z-direction-zb = 0 1  1 ! along the [011]  direction in the crystal coordinate system
  !++++++++++++++++++++ (011) surface +++++++++++++++++++++++++++++++++++++++++
 

Conduction band edges and wave functions

The following figures show the conduction band edges at the X point for AlAs(011) QWs embedded within GaAs.
The square of the wave functions (psi²) - shifted by their energies - are shown for a 4 nm and 8 nm quantum well.
The X band in AlAs is split due to compressive strain with respect to the GaAs(011) substrate.
The X_x band is not degenerate (1 valley at the X point).      ==> m_DOS = (m_l m_t)^1/2
The X_yz band is two-fold degenerate (2 valleys at the X point). ==> m_DOS = (m_t m_t)^1/2 = m_t
The X_yz and X_x valleys are separated due to strain by 9.4 meV, so this is only half as much as for the (001) case.
The GaAs barriers are unstrained.
Only the two lowest confined wave functions are shown.

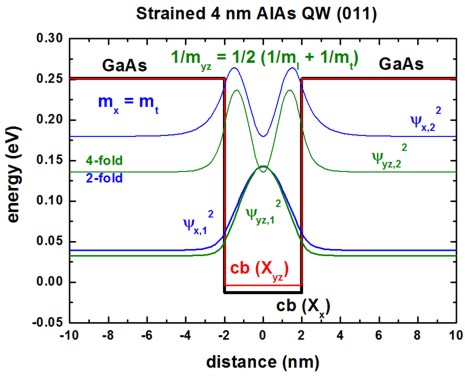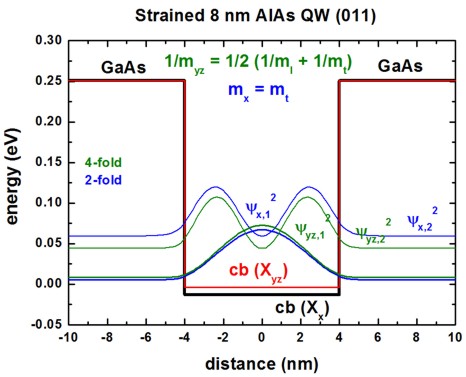
We now have different mass tensors compared to the (001) QW.
For the confinement direction z, the following mass tensor components are relevant for the Schrödinger equation:
AlAs: cb(X_x):  1/m_zz(011) = 1/m_t = 1 / 0.22
AlAs: cb(X_yz): 1/m_zz(011) = 1 / 2  ( 1/m_l + 1/m_t ) = 1 / 0.359

The mass for the two X_yz band edges is heavier than the transverse masses m_t that is relevant for the X_yz band edge.
Consequently, one expects the ground state to be determined by the heavier mass.
However, this is true only for QWs smaller than 6 nm.
For larger QW widths, the ground state is due to the other valley because here, the fact that this conduction band edge is the lowest in energy dominates.

The following figure shows the energy spectrum of a strained AlAs(011) QW as a function of QW width.
Once can clearly see the crossing of the ground state at a QW width of ~6 nm.
For the 10 nm QW, 4 states of the X_x valley and 5 states of the X_yz valleys are confined in the quantum well



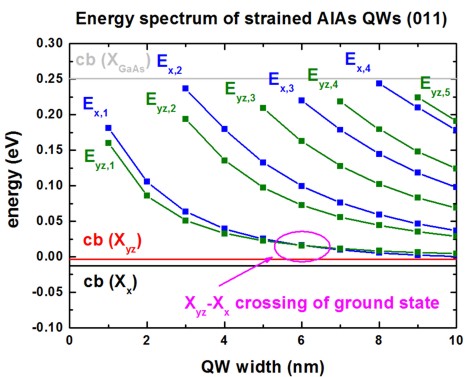
When comparing the mass tensors for (001) and (011), one can see that the mass tensor became more "isotropic" for the (011) QW (but it is still ellipsoidal).
This fact can also be seen in the energy spectrum.

Strained AlAs QW along [111] - Crossover of ground states

-> 1DAlAs_QW_4nm_111.in

Note: For strained heterostructures grown along the [111] growth direction piezoelectric fields are present! This has been neglected in this tutorial.

The following figure shows the conduction band profile and the lowest two wave functions (psi²) for the 4 nm AlAs QW grown along the [111] direction.


 

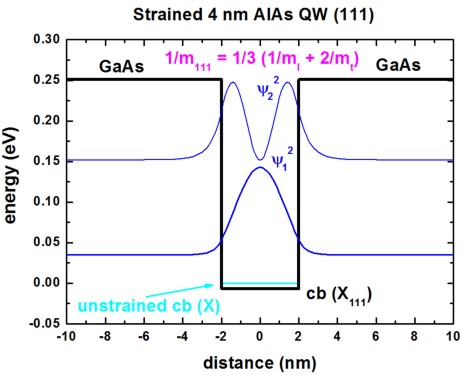
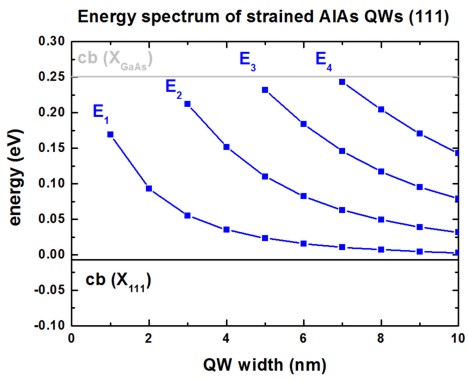
For the [111] growth direction, the three X band edges are degenerate.
In that case a crossover cannot be observed as each eigenvalue is three-fold degenerate.

AlAs: cb(X₁₁₁): 1/m_zz(111) = 1 / 3  ( 1/m_l + 2/m_t ) = 1 / 0.296

The component 1/m_zz for each grid point can be found in this file:
Schroedinger_1band/mass_tensor1D_cb003_qc001_sg001_deg001.dat
 

The following figure shows the relevant energy spectrum as a function of QW width.