nextnano3 - Tutorial
next generation 3D nano device simulator
2D Tutorial
Single-band ('effective-mass') is a special case of 8-band k.p ('8x8kp') if the
electrons are decoupled from the holes
Author:
Stefan Birner
If you want to obtain the input file that is used within this tutorial, please
submit a support ticket.
-> effective_mass_vs_8x8kp_sg_2D.in
-> effective_mass_vs_8x8kp_kp_2D.in
-> effective_mass_vs_8x8kp_density_sg_2D.in
-> effective_mass_vs_8x8kp_density_kp_2D.in
-> effective_mass_vs_8x8kp_same_mass_sg_2D.in
-> effective_mass_vs_8x8kp_same_mass_kp_2D.in
1) Single-band ('effective-mass') is a special case of 8-band k.p ('8x8kp') if the
electrons are decoupled from the holes
Input file -> 2Deffective_mass_vs_8x8kp.in
Note: This tutorial is identical to the 1D
tutorial "Single-band ('effective-mass') is a special case of 8-band k.p ('8x8kp') if the
electrons are decoupled from the holes".
The only difference is that it is 2D.
In 1D, the simulated structure is 45 nm long.
In 2D, the simulated structure is 45 nm long and 5 nm wide (y axis). Along the y
axis, we apply periodic boundary conditions to the Schrödinger equation, so that
the structure is effectively infinitely long.
Results
- The following figure shows the conduction band profile and the three
lowest (confined) eigenstates for k=0 including their charge densities (wave function
Psi²) for a 5 nm AlAs/GaAs quantum well.
1D plot of the 1D tutorial:
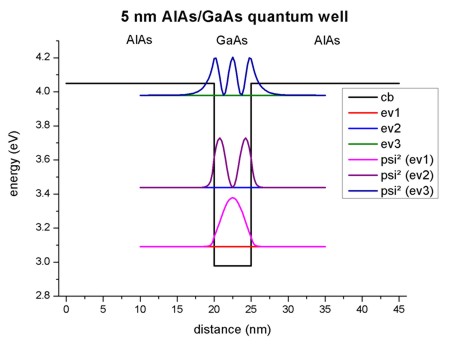
2D plot of the 2D tutorial:
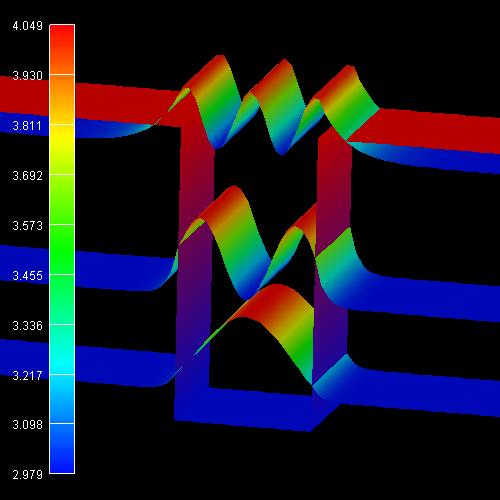
The scale on the left corresponds to the conduction band edge energies of the
barrier (4.049 eV) and the well (2.979
eV).
We want to stress that we solved a two-dimensional Schrödinger equation in 2D
and not only a one-dimensional one as in 1D.
The calculated eigenvalues can be found in the files
1D:
Schroedinger_1band/ev1D_cb001_qc001_sg001_deg001_dir _Kx001_Ky001_Kz001.dat
2D:
Schroedinger_1band/ev2D_cb001_qc001_sg001_deg001_dirper_Kx001_Ky001_Kz001.dat
dirichlet boundary condition along x
periodic boundary condition along y
| |
1D eigenvalues: |
2D eigenvalues: |
2D eigenvalues: |
2D eigenvalues (k.p): |
schroedinger-masses-anisotropic |
|
=
no |
= box |
- |
schroedinger-kp-discretization |
|
- |
- |
= box-integration |
e1 = |
3.09100 eV |
3.09100 |
3.0908 |
3.09100 |
e2 = |
3.43473 eV |
3.43473 |
3.4341 |
3.43473 |
e3 = |
3.97526 eV |
3.97526
(7th ev) |
3.9740 (5th ev) |
3.97526
(10th ev) |
effective-mass and
8x8kp lead to exactly the same eigenvalues. Also the squared wave functions
(Psi²) are identical. The squared wave functions are normalized in units of
[1/nm²] so that they integrate to 1.0 if the integration interval is over the
area from 10
nm to 35 nm along the x axis and from 0 nm to 5 nm along the y axis. (The
rectangle of the quantum cluster extends from 10 nm to 35 nm along x and from 0
nm to 5 nm along y.) Note that the probabilities Psi² are shifted by the
corresponding eigenvalues so that they fit nicely into the graph. Here, the
color dark blue corresponds to zero
probability of Psi².
Note:
Single-band
- schroedinger-masses-anisotropic = yes: Periodic boundary
conditions not implemented yet.
- schroedinger-masses-anisotropic = box: Periodic boundary
conditions implemented but do not work if the quantum cluster coincides with the
whole device volume:
'Error get_sg_material_parameters: i_material out of range.'
Thus the quantum region has to be reduced to a length of 4 nm,
i.e. from 0 to 4 nm (if the gridding is in steps of 1 nm) because 'box'
assumes that there is an additional grid point between 4 nm
and 0 nm when applying periodic boundary conditions.
- schroedinger-kp-discretization = finite-differences: Periodic boundary
conditions not implemented yet.
- schroedinger-kp-discretization = box-integration
'Error get_8x8_kp_zb_parameters: Number of point out of range.'
Thus the quantum region has to be reduced to a length of 4
nm, i.e. from 0 to 4 nm (if the gridding is in steps of 1 nm) because 'box-integration'
assumes that there is an additional grid point between 4 nm
and 0 nm when applying periodic boundary conditions.
2) Calculating the quantum mechanical density within the single-band
approximation and 8-band k.p self-consistently
Input file -> 2Deffective_mass_vs_8x8kp_density.in
Our input file contains a similar 5 nm quantum well but instead of AlAs we
take Al0.2Ga0.8As as the barrier material. However, this
time we include some n-type doping with a concentration of 1*1017 cm-3.
Only the AlGaAs region between 35 and 40 nm (along the x axis) is doped. The donor atom has a donor
level of 0.007 eV below the conduction band.
We use flow-scheme = 2, i.e.
- we solve the Poisson equation including doping to obtain the electrostatic
potential
- we use this electrostatic potential to solve Schrödinger's equation
effective-mass (single-band) approximation
- we calculate the electron density (including quantum mechanical density) that
enters the Poisson equation
- we solve the Poisson and Schrödinger equation self-consistently
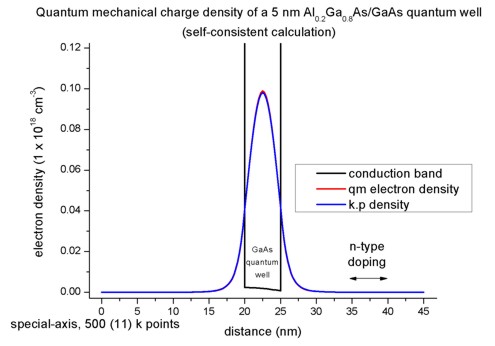
The following figure shows the conduction band profile and the lowest
eigestate as well as its probability amplitude. The chemical potential (i.e. the
Fermi level) is not shown in the figure. It is equal to 0 eV. There are no
further eigenstates that are confined inside the well. (The figure also shows
the k.p results which are identical.)
1D plot of the 1D tutorial:
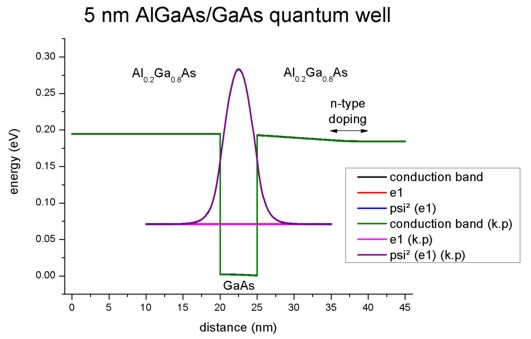
2D plot of the 2D tutorial:
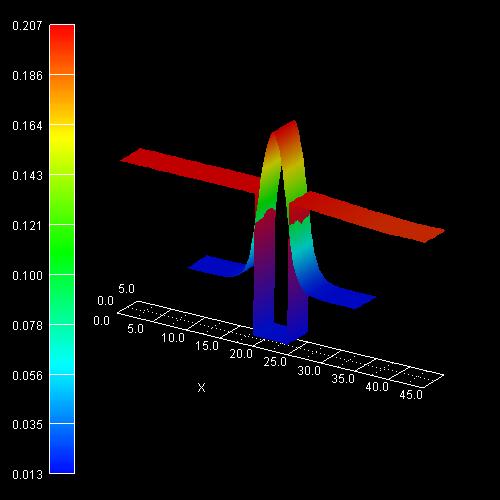
The scale on the left corresponds to the conduction band edge energies of the
barrier and the well
in units of [eV].
Note: In our example we take into account only the first quantized
eigenstate. Usually one has to sum over all (occupied) eigenstates to calculate
the quantum mechanical density.
The three-dimensional electron density of this 2D quantum structure
(homogeneous along the z direction) can be calculated
in the single-band effective-mass approximation (i.e. parabolic and isotropic bands) as
follows:
1D: n(x) = g m||,av kBT / (2 pi hbar²) |Psi1(x)|²
ln(1 + exp( (EF(x) - E1)/ (kBT) ) )
Note the squared wave function |Psi1|² must be normalized over the
length of the quantum cluster, i.e. the units are 1/m.
2D: n(x,y) = 1/2 g [ mz,av kBT / (2 pi hbar²)
]1/2 |Psi1(x,y)|² F-1/2[
(EF(x,y) - E1)/ (kBT) ]
Note the squared wave function |Psi1|² must be normalized over the
area of the quantum cluster, i.e. the units are 1/m².
(For 1D, confer also the corresponding equation in the overview section: "Purely
quantum mechanical calculation of the density".)
- g is the degeneracy factor for both spin and valley degeneracy. In our
case, the Gamma conduction band valley is not degenerate, so we have g = 2 to
account for spin degeneracy.
- Usually mz depends on the grid point (x,y), so we should have
written mz(x,y) instead of mz,av. However, this leads to
discontinuities in the quantum charge density as mz(x,y) is
discontinuous at material interfaces. A possible solution is to take an
average of all mz values in the quantum cluster weighted by the
quantum charge density (Psi²). This leads to mz,av =
0.0698246 (1D: m||,av = 0.0698240)
- kBT = 0.025852 eV (at 300 K)
- [m0 kBT / (2 pi hbar²) ]1/2 =
2.323704676 * 108 1/m
Note that: [kg VAs / (J²s²)]1/2 = [Ns²/m / (Js²)]1/2 = [N/m / J]1/2 = [1 / m²]1/2
= [1/m]
- |Psi1(x,y)|²: Probability amplitude of the wave function Psi1
of the first eigenstate.
The maximum value of |Psi1(x=22.5 nm,y)|² is 0.04247 1/nm².
This value, multiplied with the length of 5 nm (extension along the y
direction) leads to 0.21235 1/nm and compares well with the 1D result of
0.21237 1/nm.
- EF(x,y): Chemical potential (i.e. Fermi level). In our example it
is equal to zero: EF(x,y) = 0
- E1 = 0.08366 eV: energy of the first quantized state (1D: E1 = 0.07117 eV)
The Fermi-Dirac integral F-1/2 (which includes the Gamma prefactor
of the Fermi-Dirac integral) at position (x=22.5 nm,y) can be
evaluated to: F-1/2 [
(EF(x,y) - E1)/ (kBT) ] = F-1/2 [
-3.236173 ] = 0.0382551
We calculate the electron density for the grid point in the middle of the quantum well where
the maximum of the probability amplitude occurs:
=> n(x = 22.5 nm,y) = 1/2 * 2 * (0.069824)1/2 * 2.323704676*108 1/m * 0.04247 1/nm² *
0.0382551 = 9.9976 * 1022 1/m³
This number divided by the three-dimensional number density (1*1024)
leads to 0.09976, i.e. the output is in units of 1 * 1018 cm-3,
thus the density equals 0.09976 * 1018 cm-3 (1D result:
0.09893 * 1018 cm-3)
This value is in agreement with the plot of the electron density. The density
is dominated by the quantum mechanical contribution to the density. The
classical contribution is negligible (i.e. only 0.00007 * 1018 cm-3).
2D plot of the self-consistent electron charge density:
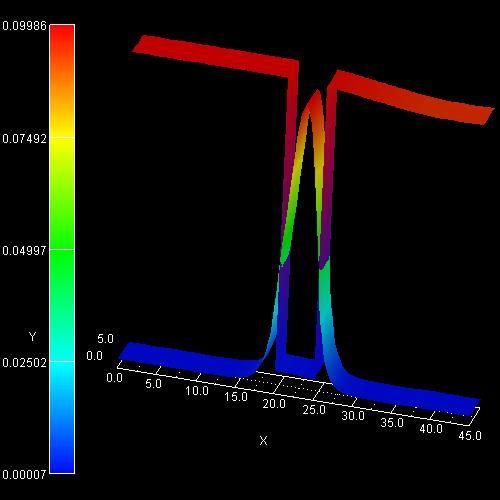
On the left side the figure shows the color map of the electron density (in
units of 1 * 1018 cm-3). Note that the color of the
conduction band edge has nothing to do with it.
Compare to the 1D plot of the corresponding 1D tutorial:
3) Calculation of the quantum mechanical density from the k.p dispersion (no
self-consistency)
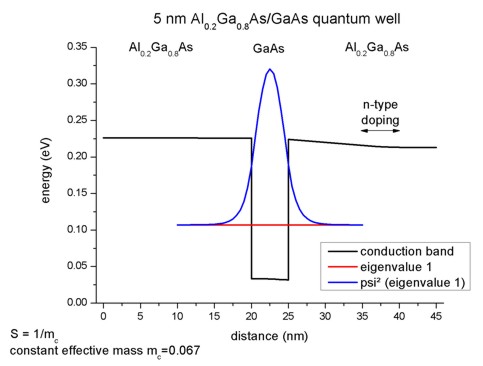
Input file -> 2Deffective_mass_vs_8x8kp_same_mass.in
To compare the k.p results with the effective-mass results it is easier
to use for both materials the same conduction band effective mass. So even for
Al0.2Ga0.8As we take the GaAs mass of 0.067 this time. The
relevant 8-band k.p parameter S is then given by S = 1/me =
1/0.067 = 14.925.
We use the same doping as in 2) but this time we use flow-scheme =
3, i.e.
- we solve the Poisson equation including doping to obtain the electrostatic
potential
- we use this electrostatic potential to solve Schrödinger's equation with both
effective-mass (single-band) approximation and 8-band k.p. As expected the
eigenvalues and wave functions coincide for these two cases. The energy of the
lowest eigenstate is E1 = 0.10707 eV (1D: E1 = 0.10707).
Here is the 1D plot of the corresponding 1D tutorial (which is identical to the
2D case):
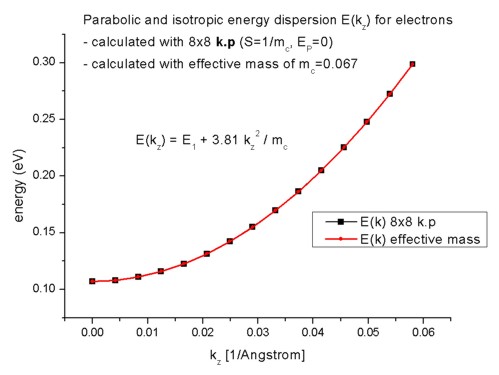
In order to calculate the k.p dispersion E(kz),
we have to solve the 8-band k.p Hamiltonian for different kz (in-plane wavevector). As our electrons in the Hamiltonian are
decoupled from the holes, we have the special case where the dispersion E(kz) is
parabolic. In 2D, the k.p dispersion is "isotropic" in any case as we
only have one direction. Thus it is possible to
plot (and calculate) the E(kz) dispersion along a line only. In 1D,
we had a 2D k space.
num-kp-parallel = 15
Our k space, i.e. k=kz,
contains 15 k points in the 1D Brillouin zone. Thus it is sufficient to integrate over the k
points that are lying along the line of the 1D Brillouin zone.
The relevant data for the E(kz) dispersion along the
kz direction is stored
in the file: Schroedinger_kp/kpar2D_dispel_ev001.dat
It contains 15 k points and the corresponding eigenvalues.
The parabolic dispersion is given by E(kz) = E1 + hbar²/2m0
kz²/mc
where hbar²/2m0 is given by 3.81 [eV Angstrom²] and
the conduction band effective mass mc is a dimensionless quantity
here in this equation. kz is given in [1/Angstrom]. E1 is
the energy of the lowest eigenstate E1 = 0.10707 eV (1D: E1 =
0.10707 eV). As expected, the
dispersion for the effective-mass approximation agrees perfectly to the 8-band
k.p case.
To calculate the k.p densities one has only one option to choose from so
far for
the integration over the 1D Brillouin zone:
method-of-brillouin-zone-integration = special-axis
= gen-dos
(not implemented yet)
= simple-integration
special-axis uses a 1D integration
along a line. The number of kz points is taken from the input file
(num-kp-parallel = 15).gen-dos calculates the density
of states (DOS) and integrates over the DOS for obtaining the k.p
density.
More details can be found in the
glossary.
The following figure compares the quantum mechanical electron charge
densities calculated with the effective-mass
approximation and with k.p.
1D plot
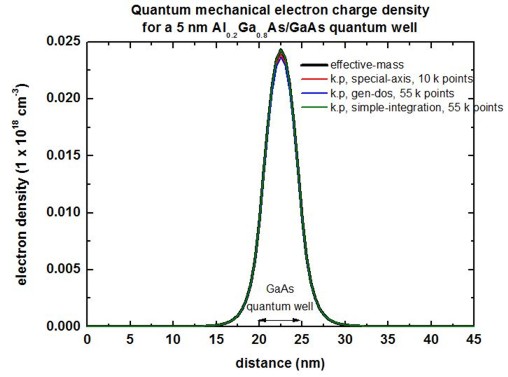
2D plot
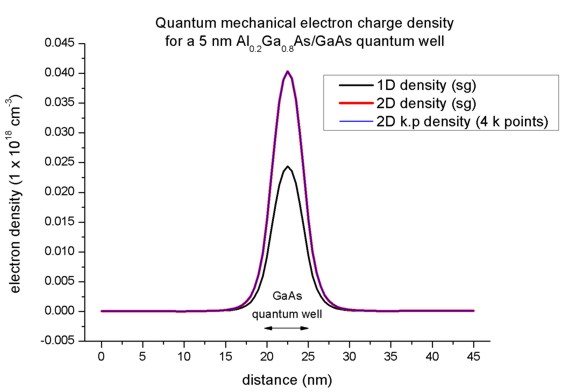
Here, the 2D k.p and single-band densities are in perfect agreement.
Only 4 kz points are necessary. However, the 2D density is different
compared to the 1D case although the conduction bands, the eigenvalues, psi² and
effective masses are in perfect agreement.
2D:
E1 = 0.10707
The Fermi-Dirac integral F-1/2 (which includes the Gamma prefactor
of the Fermi-Dirac integral) at position (x=22.5 nm,y) can be
evaluated to: F-1/2 [
(EF(x,y) - E1)/ (kBT) ] = F-1/2 [
-4.141821 ] = 0.015717538
The maximum value of |Psi1(x=22.5 nm,y)|² is 0.04265 1/nm².
This value, multiplied with the length of 5 nm (extension along the y
direction) leads to 0.21325 1/nm and compares well with the 1D result of
0.21324 1/nm.
=> n(x = 22.5 nm,y) = 1/2 * 2 * (0.067)1/2 * 2.323704676*108 1/m * 0.04265 1/nm² *
0.015717538 = 0.040320 * 1024 1/m³ = 0.04032 * 1018 1/cm³
If
F-1/2 were
0.094843, then the 2D result would be the same as the 1D one.
conduction band minimum: 0.03156 eV, conduction band maximum: 0.22592 eV
(k.p leads to the same density.)
1D:
E1 = 0.10707
The logarithm at position x can be simplified to: ln(1 + exp(- 0.10707 / 0.025852)) =
ln 1.0159 = 0.01577
Psi1²(x = 22.5 nm) = 0.21324 1/nm
=> n(x = 22.5 nm) = 0.067 * 1.07992*1017 1/m² * 0.21324 1/nm *
0.01577 = 2.43311 * 1022 1/m³ = 0.02433 * 1018 1/cm³
conduction band minimum: 0.03156 eV, conduction band maximum: 0.22592 eV
(For this tutorial example, we used k-range-determination-method =
bulk-dispersion-analysis as here the automatic determination of k-range works well because
the in-plane dispersion is the same as the bulk k.p dispersion. Note: The
new input files use 'k-max-input'
instead.)
Comments: It seems that for 2D and "box" (single-band)
the results are slightly different compared to 2D and "box-integration" (8-band
k.p).
This is a bit strange. The former results are a bit strange. This should be
checked.
|