InGaAs Multi-quantum well laser diode

Header

Files for the tutorial located in nextnano++\examples

• LaserDiode_InGaAs_1D_cl_nnp.in

• LaserDiode_InGaAs_1D_qm_nnp.in

Introduction

In this tutorial, we simulate optical emission of a 1D InGaAs multi-quantum well laser diode grown on InP substrate. The blue region, seen in Figure 2.4.88, is the separate confinement heterostructure (SCH), which forms an optical waveguide in the transverse direction to confine the emitted light (red arrow). The multi-quantum wells and SCH are clad by InP on both sides. A voltage bias is applied to the gray edges.

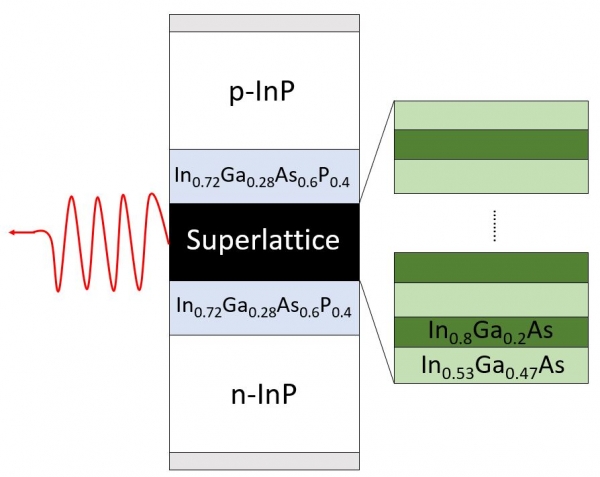
Figure 2.4.88 Structure overview

Current equation

The properties of optoelectronic devices are governed by Poisson equation, Schrödinger equation, drift-diffusion and continuity equations. We denote by $n$ and $p$ the carrier number density per unit volume. The continuity equations in the presence of creation (generation, $G$ ) or annihilation (recombination, $R$ ) of electron-hole pairs read

(2.4.25)$$\begin{array}{r}\begin{array}{rl}-e\frac{\partial n}{\partial t}+\mathrm{\nabla }\cdot (-e{\mathbf{j}}_n(\mathbf{x}))=& -e(G(\mathbf{x})-R(\mathbf{x})),\\ e\frac{\partial p}{\partial t}+\mathrm{\nabla }\cdot e{\mathbf{j}}_p(\mathbf{x})=& e(G(\mathbf{x})-R(\mathbf{x})),\end{array}\end{array}$$

where the current is proportional to the gradient of quasi Fermi levels $E_{F,n/p}(\mathbf{x})$

(2.4.26)$$\begin{array}{r}\begin{array}{rl}{\mathbf{j}}_n(\mathbf{x})& =-{\mu }_n(\mathbf{x})n(\mathbf{x})\mathrm{\nabla }{E}_{F,n}(\mathbf{x}),\\ {\mathbf{j}}_p(\mathbf{x})& ={\mu }_p(\mathbf{x})p(\mathbf{x})\mathrm{\nabla }{E}_{F,p}(\mathbf{x}).\end{array}\end{array}$$

Here the charge current has the unit of (area)${}^{-1}$(time)${}^{-1}$. ${\mu }_{n/p}$ are the mobilities of each carrier. In nextnano++, ${\mu }_{n/p}$ are determined using the mobility model specified in the input file under currents{ }. Hereafter we consider stationary solutions and set $\dot{n}=\dot{p}=0$. The governing equations then reduce to

(2.4.27)$$\begin{array}{r}\begin{array}{rl}\mathrm{\nabla }\cdot {\mu }_n(\mathbf{x})n(\mathbf{x})\mathrm{\nabla }{E}_{F,n}(\mathbf{x})& =-(G(\mathbf{x})-R(\mathbf{x})),\\ \mathrm{\nabla }\cdot {\mu }_p(\mathbf{x})p(\mathbf{x})\mathrm{\nabla }{E}_{F,p}(\mathbf{x})& =G(\mathbf{x})-R(\mathbf{x}),\end{array}\end{array}$$

which we call current equation (generation $G=0$ in the present case). The nextnano++ tool solves this equation and Poisson equation self-consistently when one specifies it in the input file as:

run{
   current_poisson{ }
}

Recombination of carriers and emission spectrum

The generation/recombination rate, $R(\mathbf{x})$, originates from several physical processes. In nextnano++, the following mechanisms are implemented (cf. recombination_model{ } )

• Schockley-Read-Hall recombination $R_{\mathrm{SRH}}$ – carrier trapping by impurities.

• Auger recombination $R_{\mathrm{Auger}}$ – a collision between two carriers results in the excitation of one and the recombination of the other with a carrier of opposite charge.

• radiative recombination $R_{\mathrm{rad}}$ – emission/absorption of a photon.

Each mechanism can be turned on and off in the input file.

Radiative recombination describes the recombination of electron-hole pairs at a position $\mathbf{x}$ by emitting a photon and is given by

(2.4.28)$$R_{\mathrm{rad}}^{spon}(\mathbf{x},E)=C(\mathbf{x})\int d{E}_h\int d{E}_{e}n(\mathbf{x},E_e)p(\mathbf{x},E_h)\delta (E_e-E_h-E),$$

where $C(x)$ [${\mathrm{cm}}^3{\mathrm{s}}^{-1}$] is the (material-dependent) radiative recombination parameter which is proportional to the one specified in the database (Radiative recombination) and $n(\mathbf{x},E),p(\mathbf{x},E)$ [${\mathrm{cm}}^{-3}{\mathrm{eV}}^{-1}$] are the charge densities as a function of energy and position.

In nextnano++, this radiative recombination whose rate is calculated as above is regarded as spontaneous emission. On the other hand, the net amount of the stimulated emission rate is given by:

(2.4.29)$$R_{rad,net}^{stim}(\mathbf{x},E)=(1-e^{\frac{E-(E_{Fn}-E_{Fp})}{k_{B}T}})R_{rad}^{spon}(\mathbf{x},E)$$

This is consistent with eq.(9.2.39) in [ChuangOpto1995]. We note that here it is assumed that photon modes occupied by one photon each, i.e. takes into account neither energy-dependent photon density of states nor Bose-Einstein distribution.

Since the radiative recombination process involves no phonons, this transition is vertical and therefore this contribution is only relevant for semiconductors with a direct band gap such as GaAs.

Absorption coefficient is calculated from $R_{rad,net}^{stim}(E)$ as

(2.4.30)$$\alpha (E)=\frac{{\pi }^2{\hslash }^3{c}^2}{n_r^2{E}^2}\frac{R_{rad,net}^{stim}(E)}{V}$$

where $n_r$ is the refractive index and $V$ is the total volume of the device. The unit is [cm${}^{-1}$]. In case of 1D simulation, calculated $R_{rad,net}^{stim}(E)$ has the unit [${\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}{\mathrm{eV}}^{-1}$] and is divided by the total length instead of the volume. This formula is consistent with eq (9.2.25) in [ChuangOpto1995].

Input file

In the beginning of the input file, we define several variables for the structure and parameters for simulation. The variable definitions are shown in Figure 2.4.89.

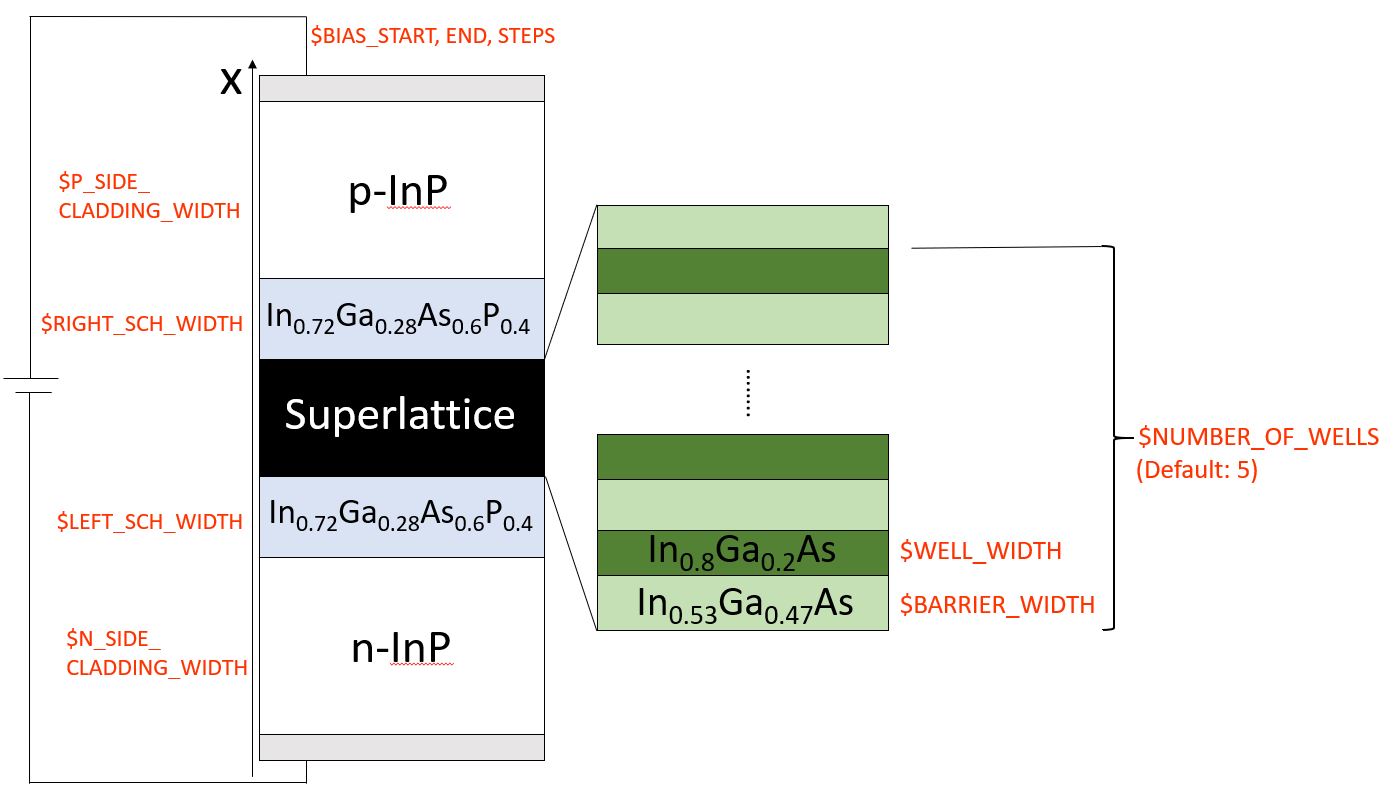
Figure 2.4.89 The definition of variables. The gray regions are contacts of 1nm thickness. $NUMBER_OF_WELLS determines the repetition of quantum wells. The program automatically sweeps the bias voltage starting from $BIAS_START until $BIAS_END, at intervals of $BIAS_STEPS.

Charge density as a function of position $n(\mathbf{x})$ is always calculated by default. On the other hand, charge density as a function of energy $n(E),p(E)$, charge density as a function of both position and energy $n(\mathbf{x},E),p(\mathbf{x},E)$ and emission spectrum are calculated when the followings are specified (see classical{ } for details):

grid{
    ...
    energy_grid{
        min_energy = -1.5                                  # Integrate from
        max_energy =  0.5                                  # Integrate to
        energy_resolution = 0.005                          # Integration resolution
    }
}


classical{
    ...
    energy_distribution{                                  # Calculation of carrier densities as a function of energy
        min_energy = -1.5                                  # Integrate from
        max_energy =  0.5                                  # Integrate to
        energy_resolution = 0.005                          # Integration resolution
        only_density_quantum_regions = yes
    }

    energy_resolved_density{
        only_density_quantum_regions = yes
        output_energy_resolved_densities{}
    }


    semiclassical_spectra{
        output_spectra{

            emission = yes
            gain = yes
            absorption = yes

            spectra_over_energy = yes
            spectra_over_wavelength = yes
            spectra_over_frequency = yes
            spectra_over_wavenumber = yes

            photon_spectra = yes
            power_spectra = yes

        }
        output_photon_density = yes
        output_power_density = yes
    }
}

The mobility model and recombination models for the current equation are specified in currents{ } as

currents{
    mobility_model = constant
#  mobility_model = minimos
    recombination_model{
        SRH         = yes          # 'yes' or 'no'
        Auger       = yes          # 'yes' or 'no'
        radiative   = yes          # 'yes' or 'no'
    }
}

The run{ } flag specifies which equations to solve. This is the main difference between LaserDiode_*_qm_nnp.in and LaserDiode_*_cl_nnp.in.

# qm
run{
    strain{ }                                        # solves the strain equation
    current_poisson{                                # solves the coupled current and Poisson equations self-consistently
        output_log     = yes
        iterations     = 1000
        alpha_fermi = 0.5
    }
    quantum_current_poisson{                        # solves the Schrödinger, Poisson (and current) equations self-consistently
        iterations     = 1000
        alpha_fermi    = 0.9
        residual       = 1e6
        residual_fermi = 1e-8
        output_log     = yes
    }
}

# cl
run{
    strain{ }                                        # solves the strain equation
    current_poisson{                                # solves the coupled current and Poisson equations self-consistently
        output_log     = yes
        iterations     = 1000
        alpha_fermi    = 0.7
        residual_fermi = 1e-10
    }
}

In this case nextnano++ first solves the strain equation from the crystal orientation to decide the polarization charges (piezoelectric effect) and shifted band edges. Then the program solves the coupled current-Poisson-Schrödinger equations in a self-consistent way (input file: LaserDiode_InGaAs_1D_qm_nnp.in). For the classical calculation (LaserDiode_InGaAs_1D_cl_nnp.in), quantum_current_poisson{ } is commented out to restrict the calculation to the current-Poisson equations only.

Results

Band structure

The band structure and emission power spectrum of the system are stored in bandedges.dat. Figure 2.4.90 shows the case for the bias $0.2$ V. Here the quasi Fermi level of electrons is lower than the quantum wells.

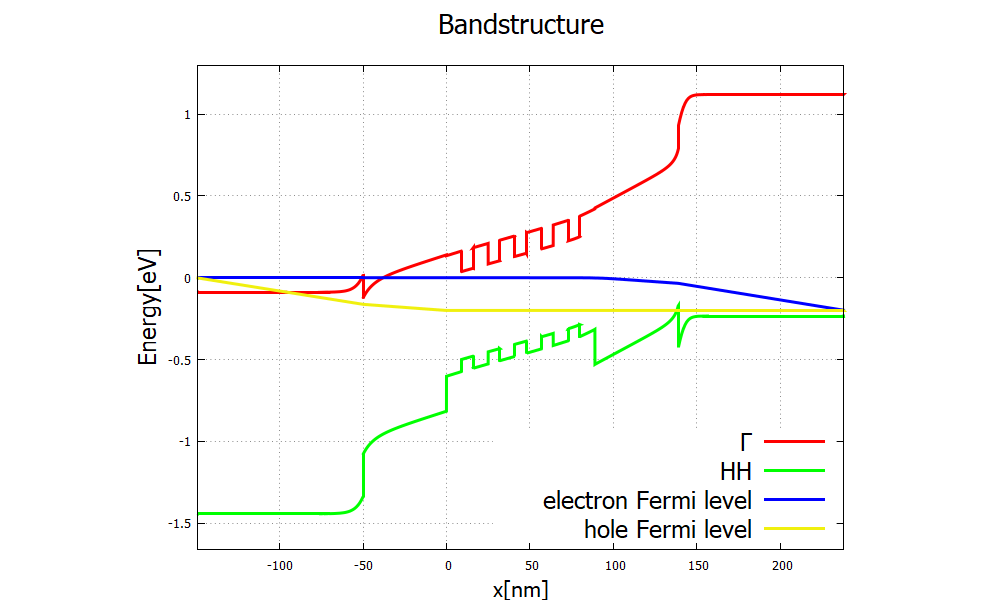
Figure 2.4.90 Band structure of the laser diode system for a low bias of $0.2$ V.

For the bias $0.8$ V (Figure 2.4.91), in contrast, it lies above the red line, allowing electrons to flow into the quantum wells. An electron trapped in the quantum wells is likely to recombine with a hole in the valence band, emitting a photon. In the input file \Optical\emission_photon_density.dat, one can see that the photons are emitted from this active region (not shown). Figure 2.4.99 shows the emission spectrum in this case. When the bias is too small, e.g. Figure 2.4.90, the intensity is much smaller, as can be seen in Figure 2.4.103.

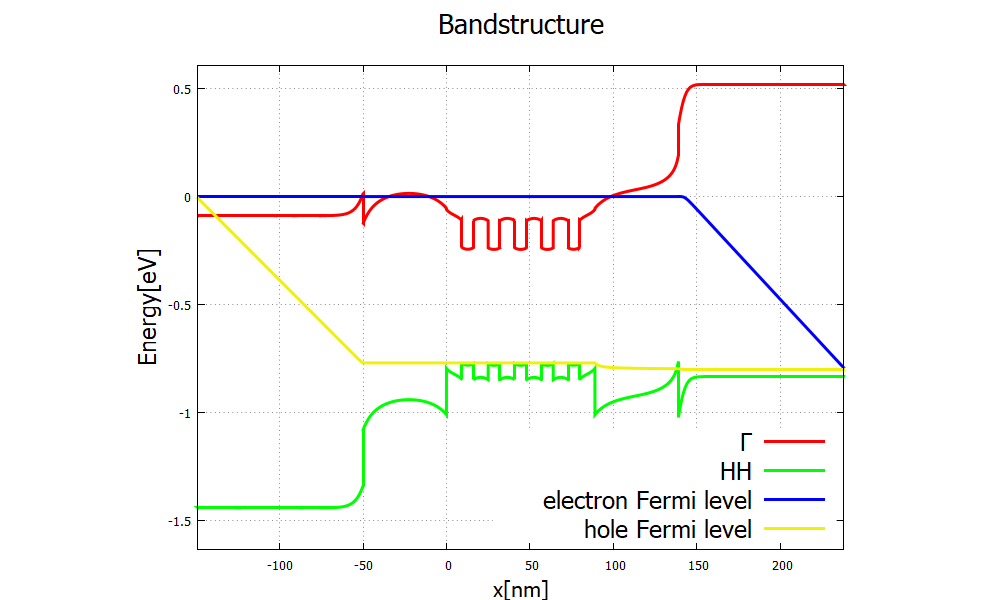
Figure 2.4.91 Band structure for a high bias $0.8$ V. Electrons flowing from the left and holes from the right recombine in the active zone (multi-quantum well structure).

Energy eigenstates and eigenvalues

In the input file LaserDiode_InGaAs_1D_qm_nnp.in, the single-band Schrödinger equation is coupled to the current-Poisson equation and solved self-consistently. The wave functions of electrons and holes along with eigenvalues are written in \Quantum\probabilities_shift_quantum_region_Gamma_0000.dat and \Quantum\probabilities_shift_quantum_region_HH_0000.dat (Figure 2.4.92 and Figure 2.4.93). The light hole and split-off states are out of the quantum wells and not of our interest here.

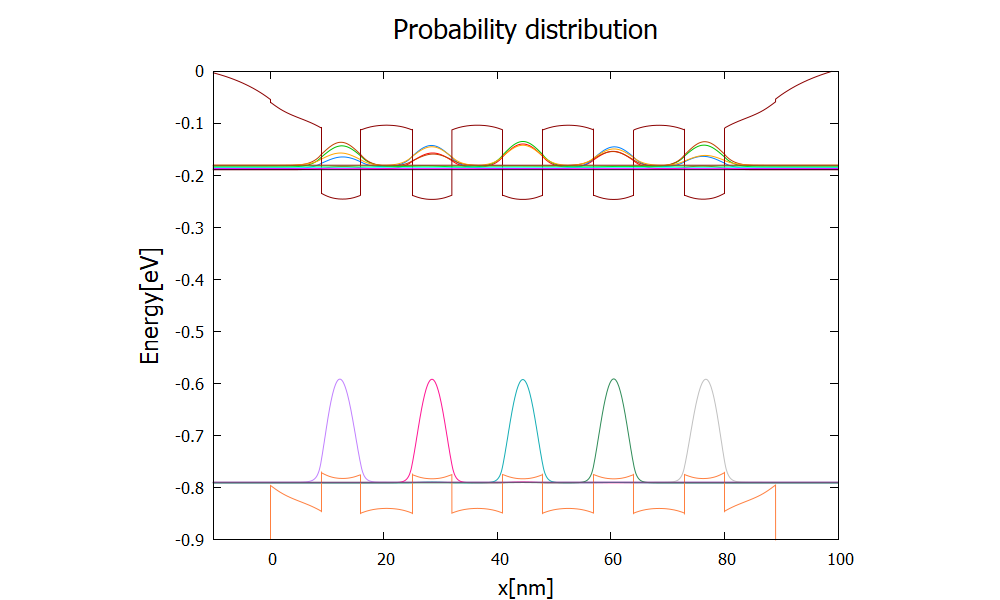
Figure 2.4.92 Probability distribution $|\psi (x){|}^2$ of the lowest localized modes of electrons and holes for the band structure Figure 2.4.90. Horizontal lines are the corresponding eigenenergies.

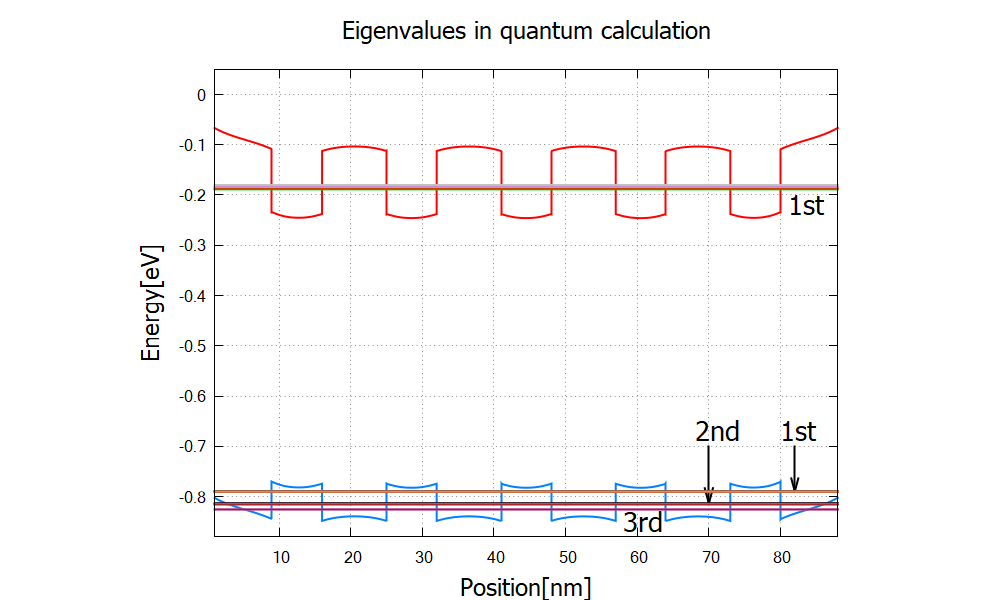
Figure 2.4.93 Eigenvalues of the Gamma-band up to 5th and heavy-hole-band states up to 13th in relation to band edges. The Eigenvalues above these are higher than the barrier energy of the quantum wells. The Gamma band has single “miniband”, whereas the heavy-hole band has three. The 1st heavy-hole miniband consists of the 1st~5th eigenvalues, the 2nd heavy-hole miniband consists of the 6th~11th eigenvalues and the 3rd consists of the 12th and 13th eigenvalues.

Charge densities

We can find the energy-resolved charge density $n(x,E)$ and $p(x,E)$ in the output electron_density_vs_energy.fld and hole_density_vs_energy.fld. The following figures represent $n(x,E)$ and $p(x,E)$ [${\mathrm{cm}}^{-3}{\mathrm{eV}}^{-1}$] with respect to the band edges and quasi-Fermi levels at bias 0.2, 0.4, 0.6, 0.8 and 1.0 V. We can see that the carrier densities around the quantum wells increase as the bias increases.

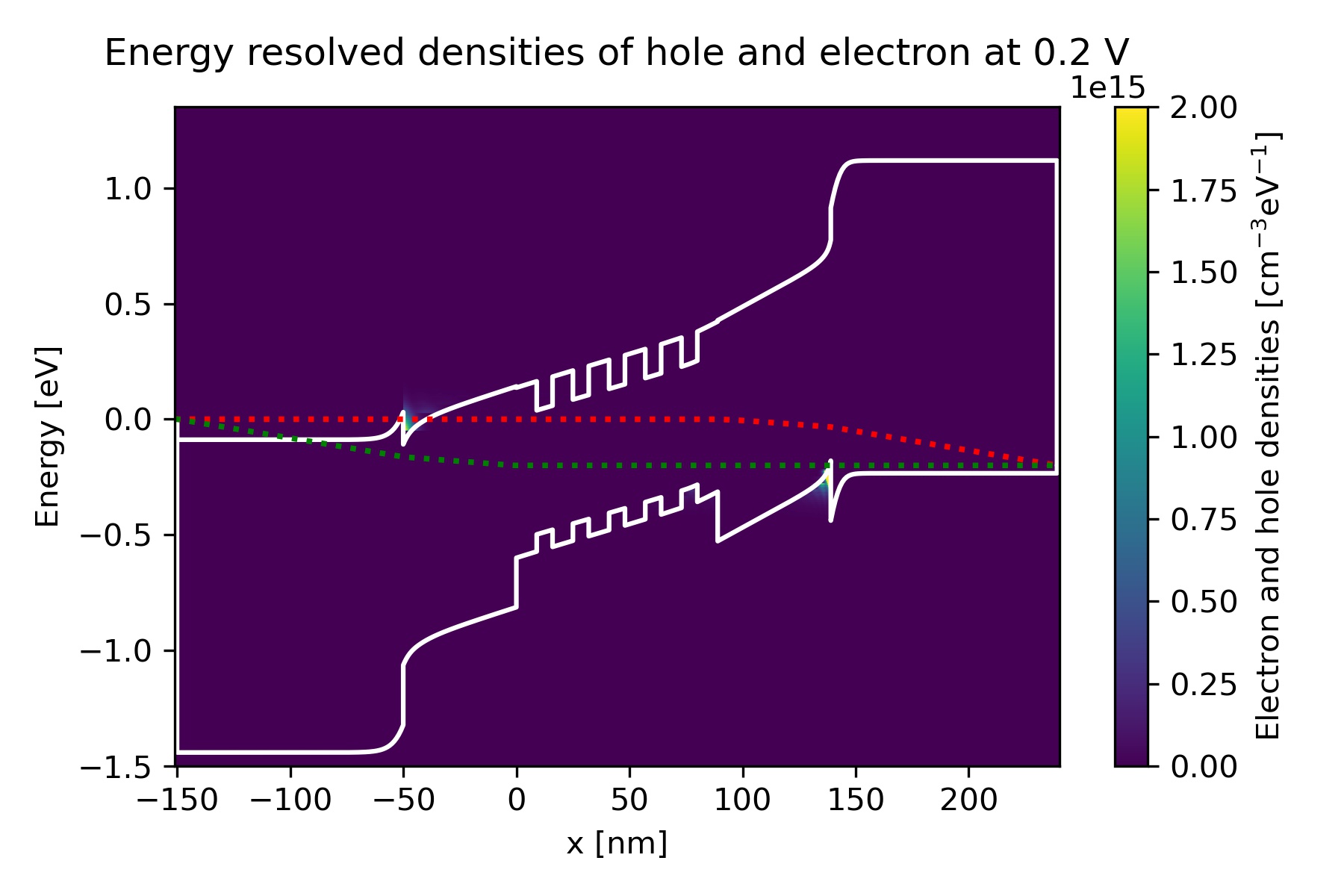
Figure 2.4.94 Energy-resolved electron and hole density, Gamma conduction band edge, HH valence band edge and quasi-Fermi levels at bias 0.2 V in quantum calculation.

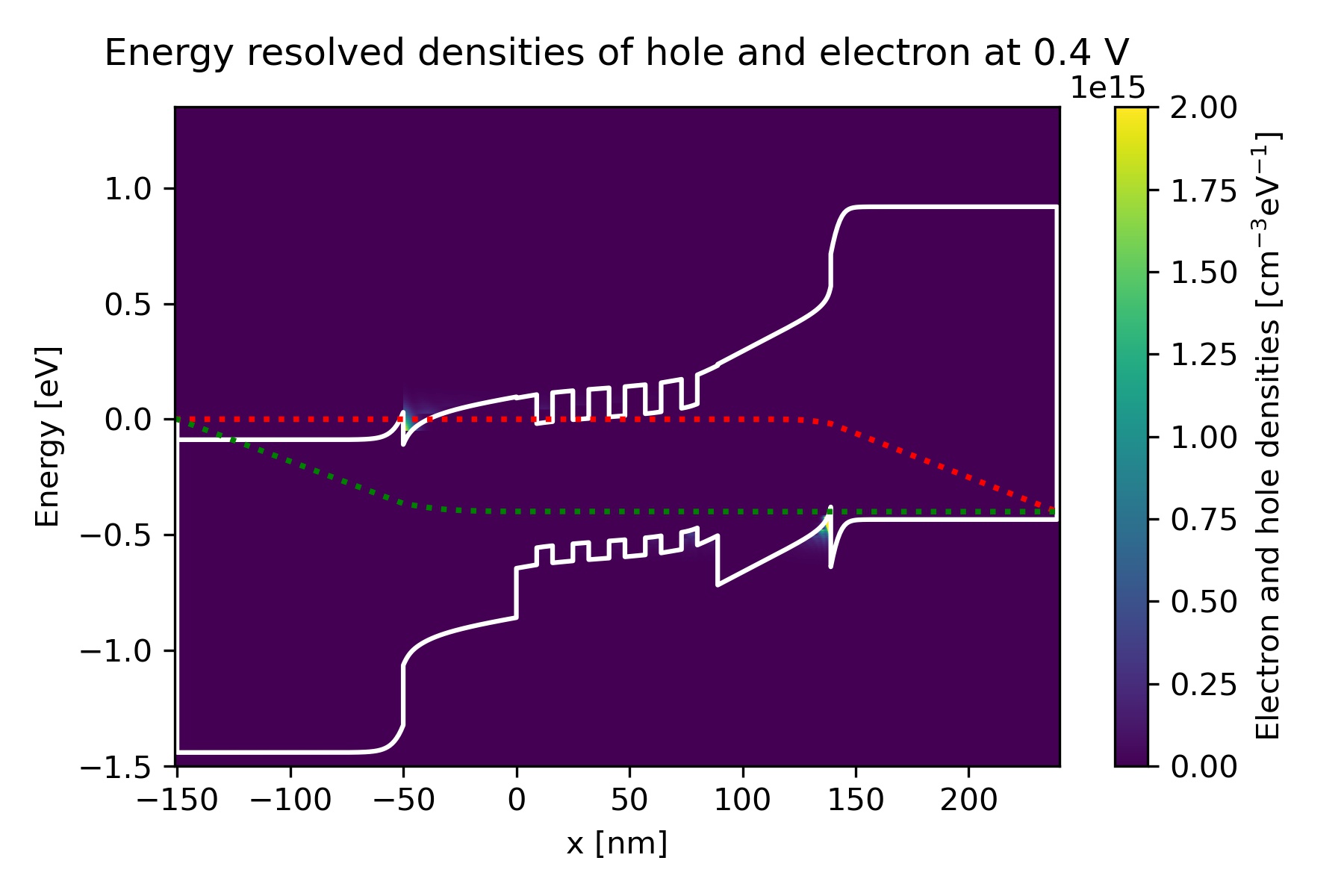
Figure 2.4.95 Energy-resolved electron and hole density, Gamma conduction band edge, HH valence band edge and quasi-Fermi levels at bias 0.4 V in quantum calculation.

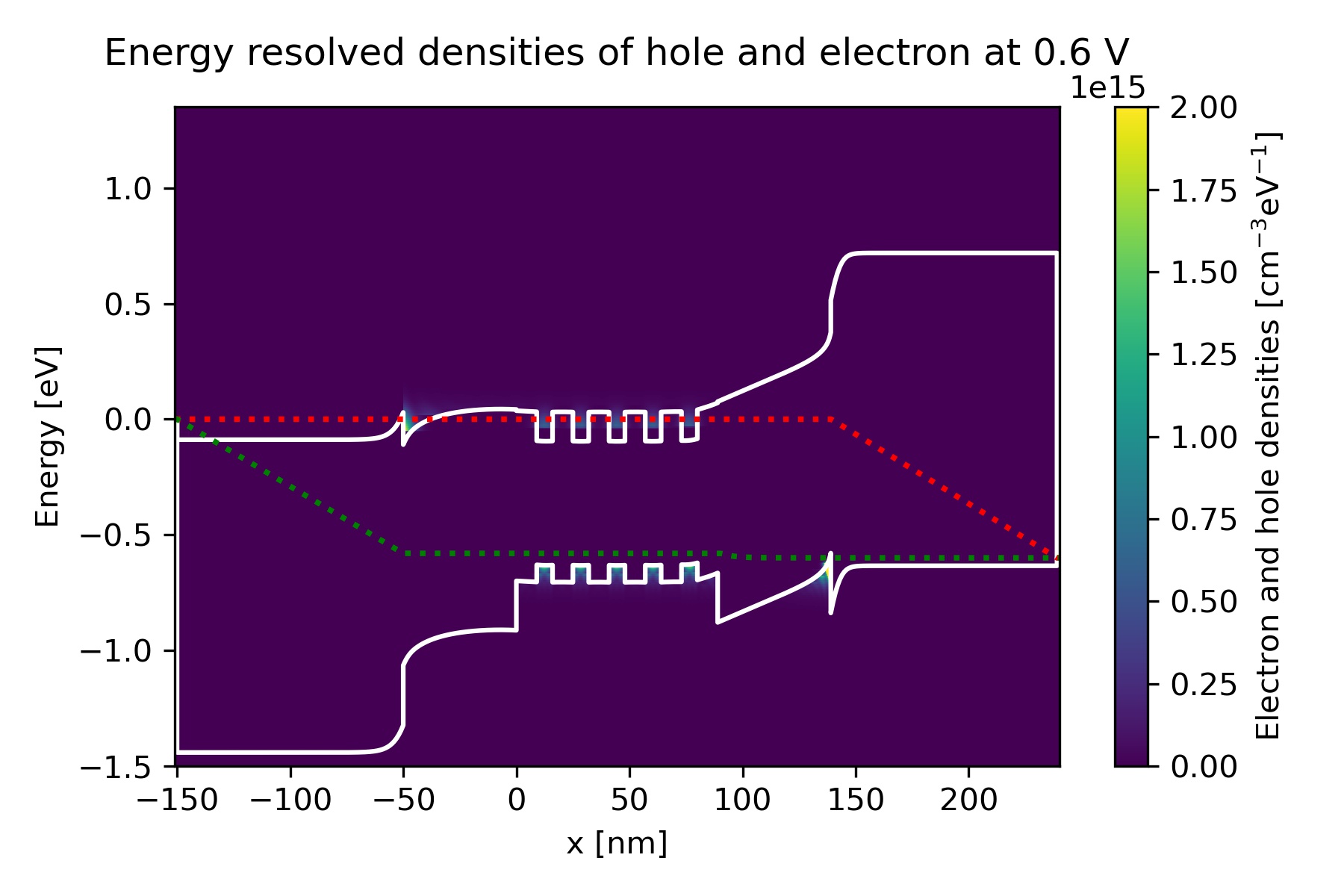
Figure 2.4.96 Energy-resolved electron and hole density, Gamma conduction band edge, HH valence band edge and quasi-Fermi levels at bias 0.6 V in quantum calculation.

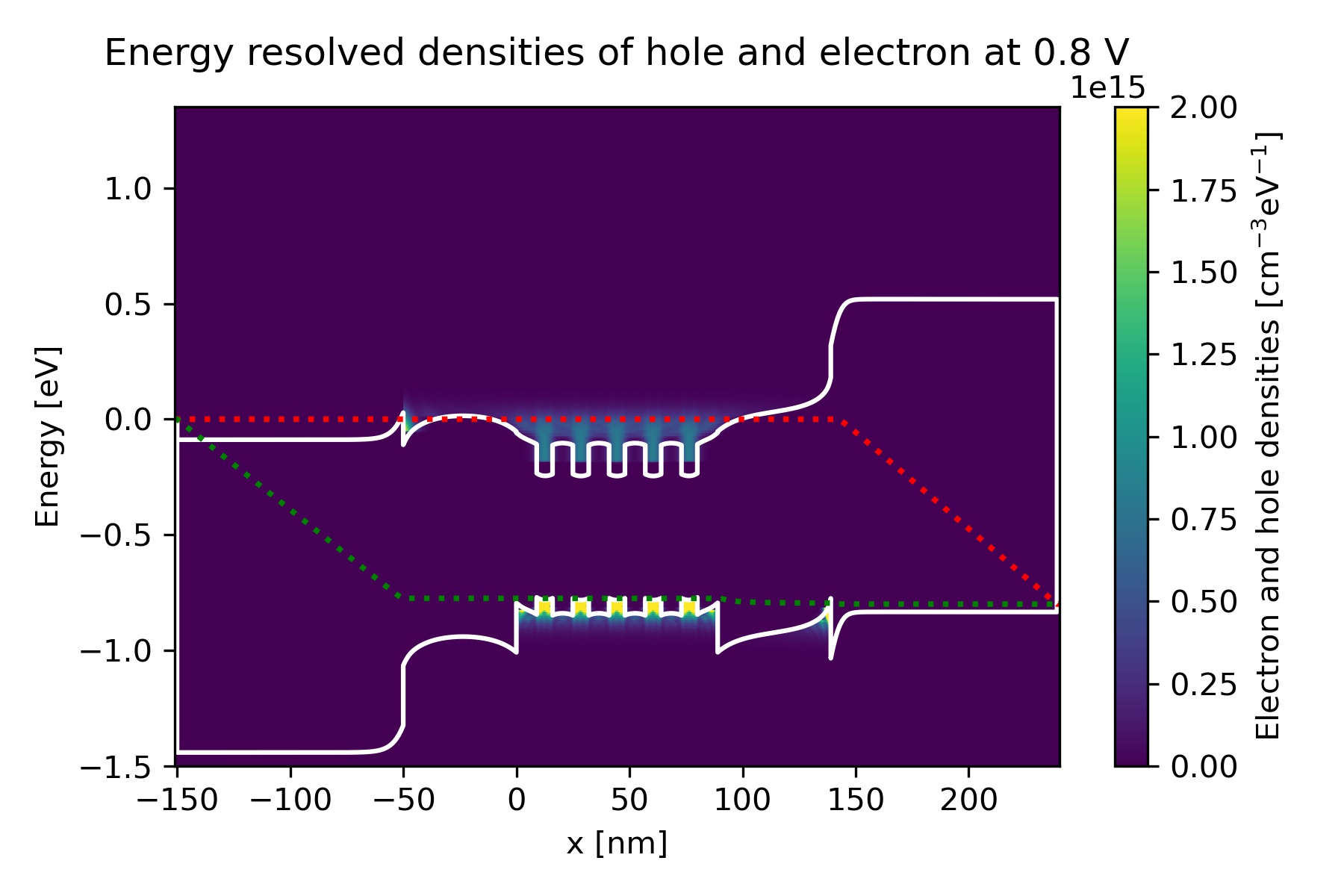
Figure 2.4.97 Energy-resolved electron and hole density, Gamma conduction band edge, HH valence band edge and quasi-Fermi levels at bias 0.8 V in quantum calculation.

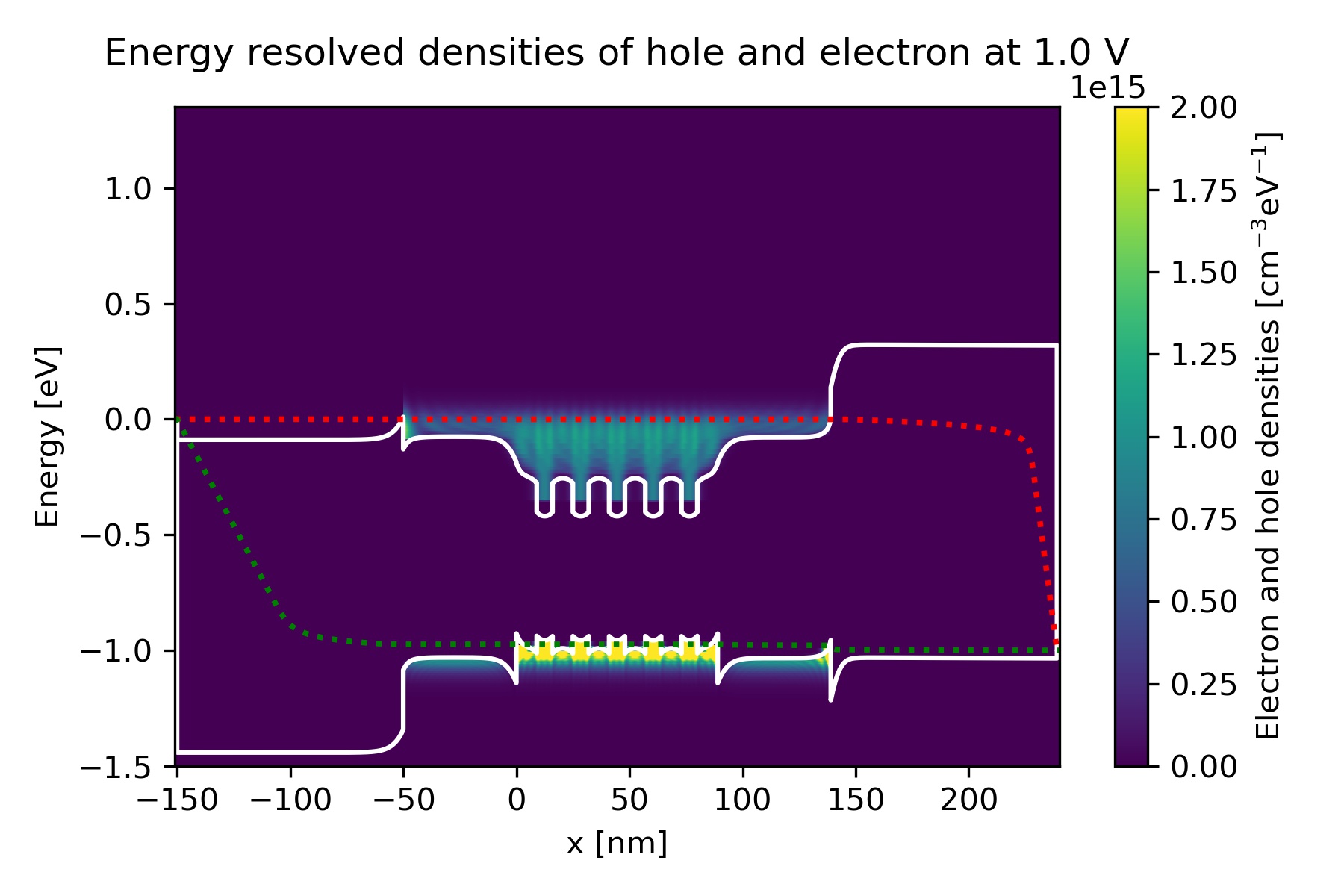
Figure 2.4.98 Energy-resolved electron and hole density, Gamma conduction band edge, HH valence band edge and quasi-Fermi levels at bias 1.0 V in quantum calculation.

Note

These graphs are generated by nextnanopy.

We also have the charge densities integrated over the device $n(E),p(E)$ [${\mathrm{cm}}^{-2}{\mathrm{eV}}^{-1}$] and energy $n(x),p(x)$ [${\mathrm{cm}}^{-3}$].

$n(E)$ and $p(E)$ with and without quantum calculation shows different features due to the discretization of energy levels in quantum wells. This is shown in integrated_densities_vs_energy.dat.

Figure 2.4.99 illustrates the population inversion in stationary (quasi-equilibrium) state of the device under bias. Solid and dashed lines are for quantum and classical calculations, respectively. The black arrows mark the relevant energies of the structure 4 at bias of 0.8 V. The hole density is shown in Figure 2.4.100 with higher resolution.

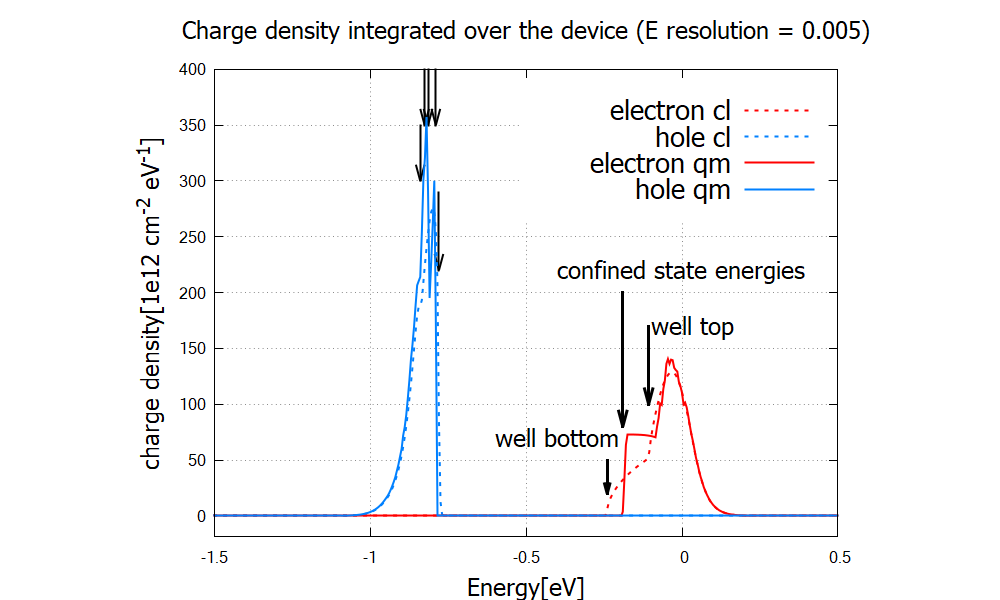
Figure 2.4.99 Electron (red) and hole (blue) densities integrated over the device as a function of energy.

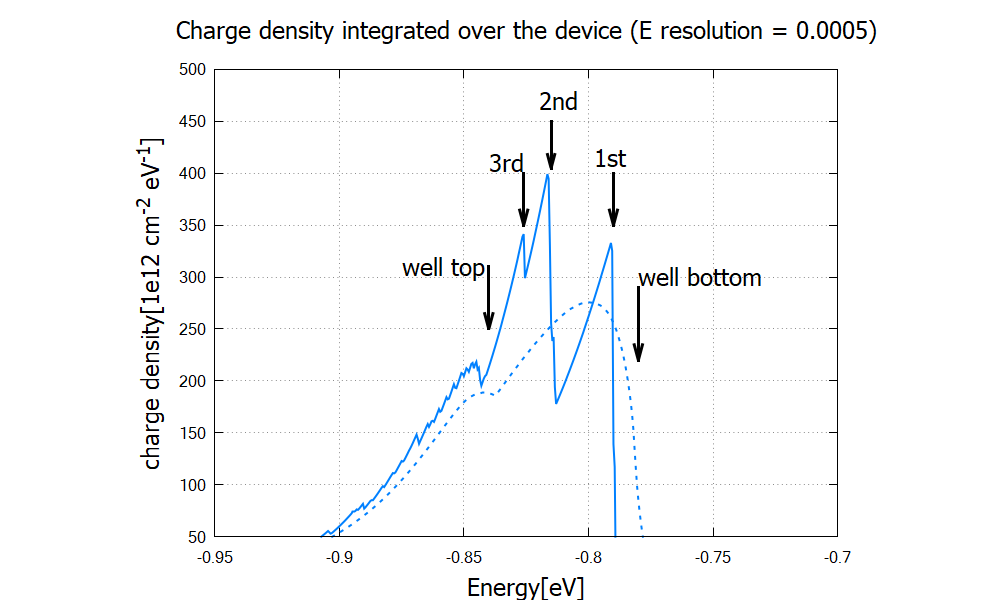
Figure 2.4.100 Hole density integrated over the device from classical (dashed) and quantum (solid) calculation.

The energy resolution in Figure 2.4.100 has been increased by a factor of 10 from Figure 2.4.99.

Note

Although these charge densities either with variable $E$ or $x$ are both obtained by integrating $n(x,E)$ and $p(x,E)$ over the corresponding variable, these are independently calculated in nn++ simulation. Hence it is possible to turn off the calculation only for $n(x,E)$ and $p(x,E)$ calculating the integrated charge densities. In this case it runs much faster and needs much less memory.

Emission and absorption spectra

The spontaneous and stimulated emission spectra are written in \Optical\semiclassical_spectra_photons.dat and \Optical\stim_semiclassical_spectra_photons.dat, respectively (Figure 2.4.101). The peak is at around 0.7-0.8eV, which is consistent with the charge distribution in Figure 2.4.99. The stimulated emission does not occur above the quasi Fermi level separation, $E_{Fn}-E_{Fp}$.

The formulas used for the calculation in the source code are specified above: Recombination of carriers and emission spectrum.

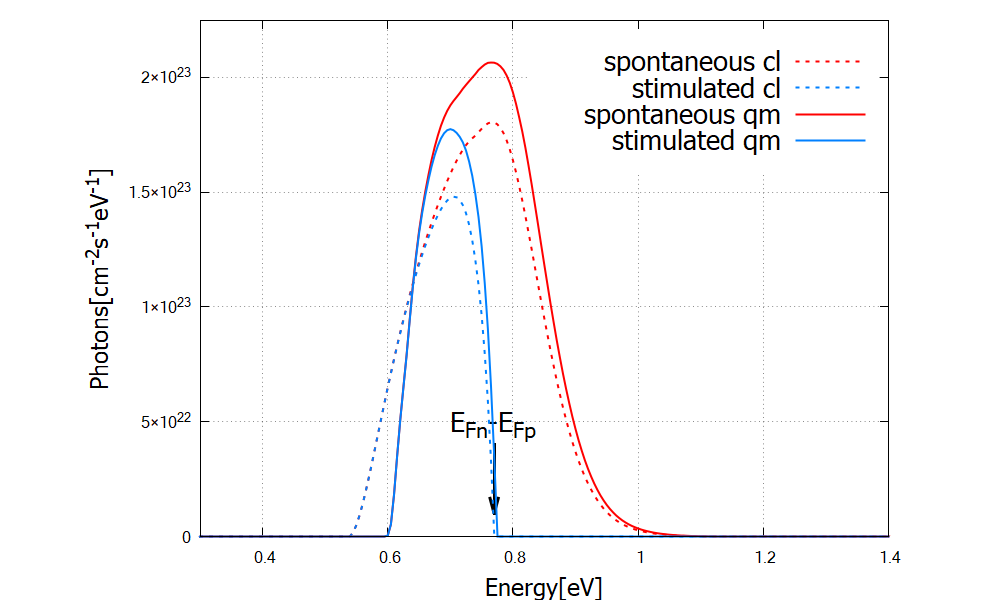
Figure 2.4.101 Emission spectrum of the laser diode for the bias $0.8$ V.

The absorption spectra are calculated as

$$\alpha (E)=\frac{{\pi }^2{\hslash }^3{c}^2}{n_r^2{E}^2}\frac{R_{rad,net}^{stim}(E)}{V}$$

where $n_r$ is the refractive index and $V$ is the total volume of the device. The unit is [cm${}^{-1}$]. In case of 1D simulation, calculated $R_{rad,net}^{stim}(E)$ has the unit [${\mathrm{cm}}^{-2}{\mathrm{s}}^{-1}{\mathrm{eV}}^{-1}$] and is divided by the total length instead of the volume. This formula is consistent with eq (9.2.25) in [ChuangOpto1995].

The absorption spectra $\alpha (E)$ and gain spectra $g(E)$ are essentially the same quantity with opposite signs,

$$\alpha (E)=-g(E)$$

These are by definition independent of the initial photon population. Please note that the gain spectrum in nextnano++ is cut off where it is negative. For details, see classical{ }.

The spectrum changes its sign at the energy $E_{Fn}-E_{Fp}$, that is, the separation of the quasi Fermi levels. According to the output bandedges.dat, this value is -0.0001-(-0.7702)=0.7701eV. The following result has been calculated classically. We also get qualitatively consistent results from quantum mechanical simulation.

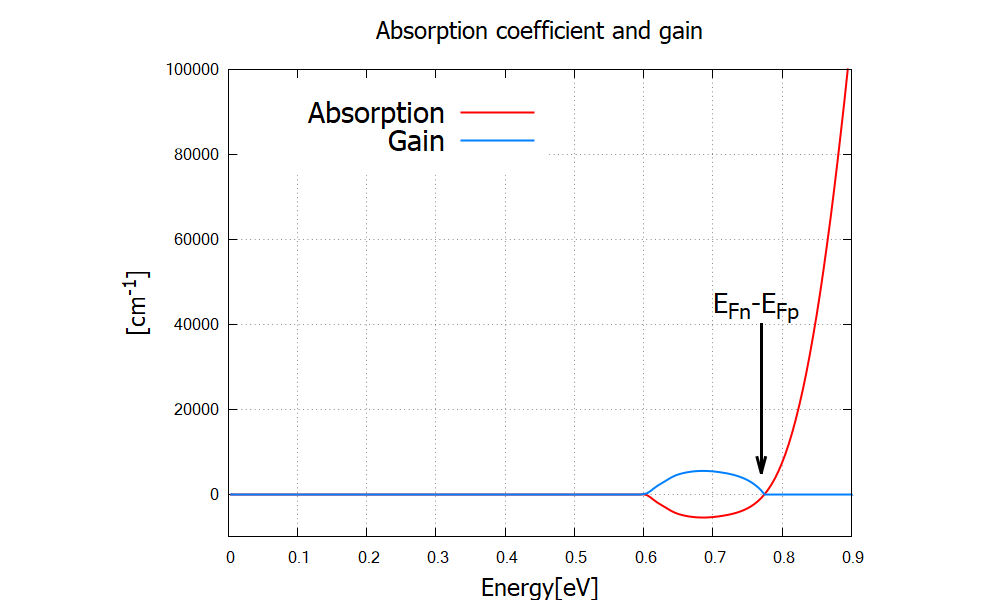
Figure 2.4.102 Classically calculated absorption and gain spectra. The sign of the spectrum switches at the energy corresponding to the quasi Fermi-level separation in the active region.

Current and internal quantum efficiency

The output file IV_characteristics.dat contains right- and left-contact current in unit of [Acm${}^{-2}$]. In the present case, the right-contact current is hole current, whereas the left-contact current is electron current. In Figure 2.4.102, we compare the hole current and photocurrent.

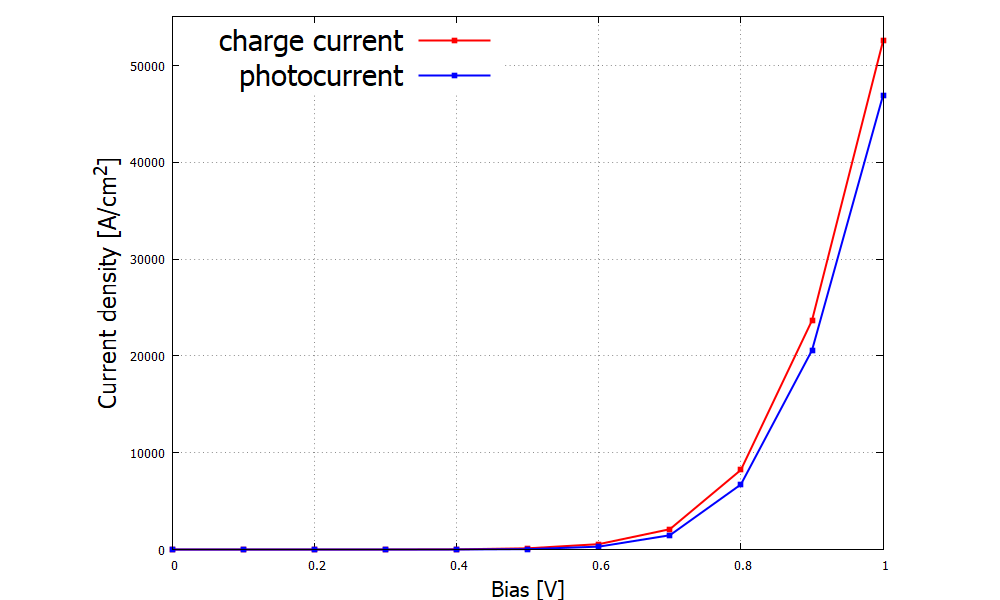
Figure 2.4.103 Charge current and photocurrent as a function of bias voltage (IV characteristics).

Figure 2.4.103 clearly shows the consequence of the difference in band structures Figure 2.4.90 and Figure 2.4.91. The holes and electrons recombine in the multi-quantum well layers, emitting one photon per electron-hole pair. The efficiency of conversion from charge current into photocurrent is called the internal quantum efficiency

(2.4.31)$$\eta =\frac{I_{\mathrm{photon}}}{I_{\mathrm{charge}}}.$$

This quantity is written in internal_quantum_efficiency.dat and shown in Figure 16.

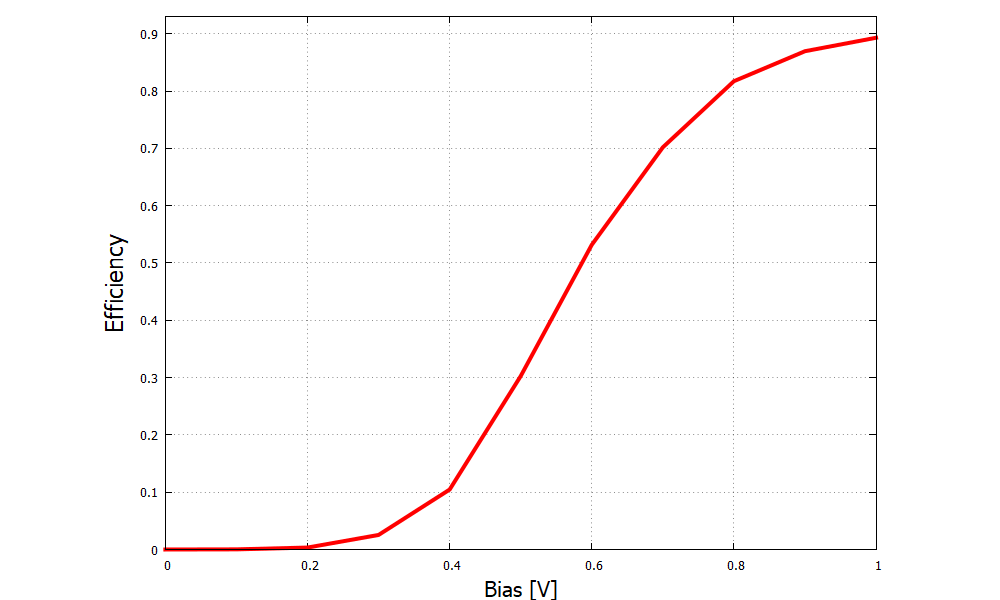
Figure 2.4.104 Conversion efficiency of the InGaAs laser diode.

Last update: 16/07/2024