Energy dispersion of a cylindrical shaped GaN nanowire¶

Input files:

2DGaN_nanowire_nnp.in

Scope:
In this tutorial we study the electron and hole energy levels of a two-dimensional freestanding $GaN$ nanowire of cylindrical shape. We aim to reproduce results of [ZhangXia2006].

Output files:

bias_00000\Quantum\Dispersions\dispersion_quantum_region_kp6_path_as_in_input_file.dat

bias_00000\Quantum\probabilities_quantum_region_kp6_00000.fld

Introduction¶

We assume a cylindrical shaped $GaN$ nanowire (wurtzite structure) that has a radius of 2 nm with infinite barriers so that the wave functions are zero at the nanowire boundary. This assumption is consistent to [ZhangXia2006]. The $GaN$ nanowire is shown in red in Figure 2.5.9.35. The $GaN$ nanowire is discretized on a mesh with a grid resolution of 0.05 nm.

../../../_images/GaN_nanowire_material_grid.jpg — Figure 2.5.9.35 $GaN$ nanowire structure.¶

Electrons¶

Figure 2.5.9.36 shows the electron states as a function of $k$ of the $GaN$ nanowire. It is in excellent agreement with Fig. 1 of [ZhangXia2006]. All states are two-fold degenerate due to spin. In addition, the 2nd and 3rd state are degenerate, as well as the 4th and the 5th. The ground state has quantum number $L$ = 0. For $L \neq$ 0, the states are degenerate due to $L$ = $\pm$ 1. The energy levels increase with increasing $k$ as quadratic terms of $k$ (parabolic dispersion).

Technical details: We calculated the electron energy levels at $k_x$ = 0 with nextnano++ numerically by solving the 2D single-band Schrödinger equation. The parabolic dispersion for $k_x \neq$ 0 has been calculated analytically using

\[E_i(k_x) = E_i + \frac{\hbar^2 k_x^2}{2m^*}\]

i.e. not with nextnano++. The eigenvalues for $k_x$ = 0 can be found in the following file: bias_00000\Quantum\energy_spectrum_quantum_region_Gamma_00000.dat

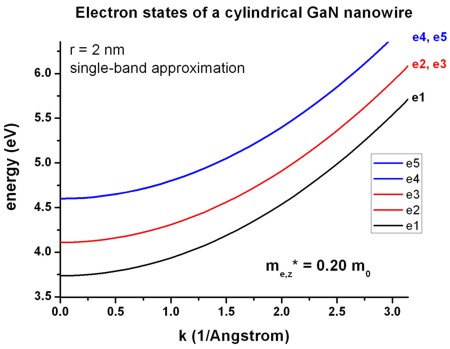
../../../_images/el_dispersion.jpg — Figure 2.5.9.36 Energy dispersion $E(k)$ of electron states.¶

The wave function ($\Psi^2$) of the electron ground state at $k$ = 0 is shown in Figure 2.5.9.37.

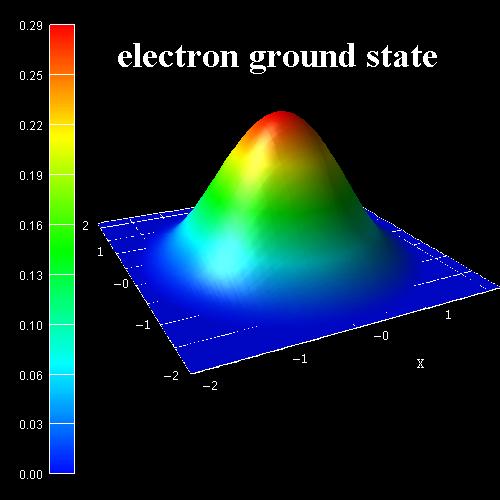
../../../_images/el_groundstate.jpg — Figure 2.5.9.37 $\Psi^2$ of electron ground state.¶

Holes¶

The following figures show the ground state wave function (psi^2) of the hole (Figure 2.5.9.38) and the 1st excited hole state (Figure 2.5.9.39) as calculated within the 6-band k.p approximation at $k$ = 0. According to the above cited paper, the right figure would be the ground state for $GaN$ nanowires with a radius $r$ < 0.7 nm. Because our nanowire has a radius of 2 nm, the ground state wave function is according to the left figure. Following [ZhangXia2006], this means that the probability for electron-hole transitions (e1 - h1) is not very high at a radius of 2 nm because the wave functions don’t have much overlap and the electron ground state has $L$ = 0, whereas the hole ground state has $L$ = $\pm$ 1 (dark exciton effect).

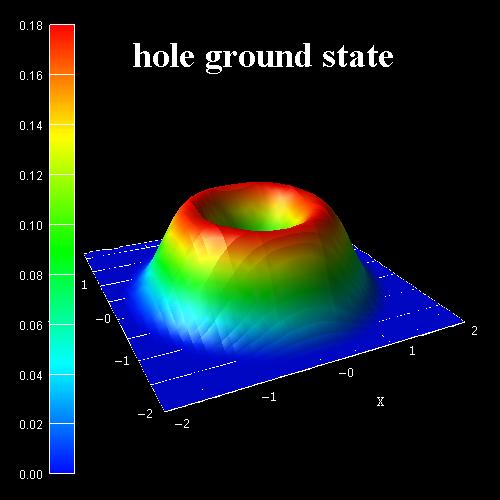
../../../_images/hl_groundstate.jpg — Figure 2.5.9.38 $\Psi^2$ of hole ground state.¶

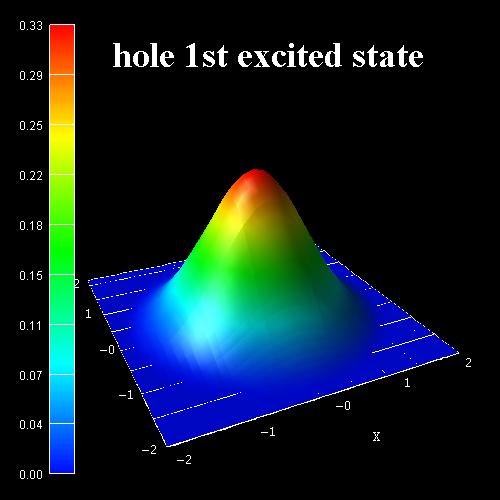
../../../_images/hl_excitedstate.jpg — Figure 2.5.9.39 $\Psi^2$ of 1st excited hole state.¶

Figure 2.5.9.40 shows the hole states as a function of $k$ of the $GaN$ nanowire as calculated with 6-band k.p theory. It corresponds to Fig. 2 and Fig. 3 of the paper of [ZhangXia2006]. Note that the authors assumed the hole energies to be positive. All states are two-fold degenerate, i.e. h1 = h2, h3 = h4, h5 = h6, …

The nextnano++ results are a bit different. Several reasons could explain this:

The authors use the “cylindrical approximation” for the k.p parameters. However, the parameters that they are citing are not exactly cylindrical. Thus, for our calculations, we had to employ the parameters that they were citing (without making use of the cylindrical approximation).

Our cylinder does not have exactly cylindrical symmetry. It is approximated to be cylindrical by a rectangular grid with a grid resolution of 0.05 nm.

For the k.p parameters that are given in [ZhangXia2006], it must hold that

\[A_5 = \frac{1}{2} (L_1 - M_1)\]

is equal to

\[A_5 = \frac{1}{2} N_1.\]

However, they differ by 0.0064.

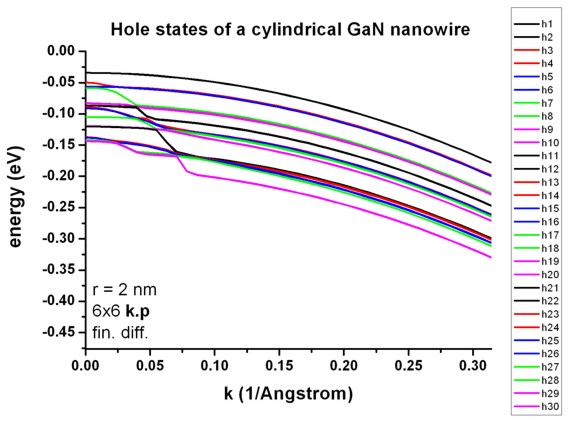
../../../_images/hl_dispersion_findiff.jpg — Figure 2.5.9.40 Energy dispersion $E(k)$ of hole states.¶

The data that has been plotted in Figure 2.5.9.40 is contained in this file: bias_00000\Quantum\Dispersions\dispersion_quantum_region_kp6_lines_type1_00-1_001.dat

In the input file, one can specify the number of $k_{||}$ = $k_x$ points.

quantum{
    region{
        ...
        kp_6band{
            dispersion{
                line{
                    name = "lines"
                    spacing = 2 * $k_max / $number_of_k_parallel_points # Unit: [nm-1].
                    k_max = $k_max                                      # specifies a maximum absolute value (radius) for the k-vector. Unit: [nm-1].
                }
            }
        }
    }
}

Note that e.g. $number_of_k_parallel_points = 41 means 14 minutes CPU time (Intel i5, 2015). If one uses only 1, then one only calculates the k.p states at $k_x$ = 0 and the calculation takes less than a minute.

[ZhangXia2006] used the following 6-band k.p parameters:

Crystal field and spin-orbit splitting energies:

\[\Delta_{cr} = 0.021\]

\[\Delta_{so} = 0.018\]

“Dresselhaus” parameters:

[ZhangXia2006]

nextnano++

$L$ = 6.3055

$L_1$ = -6.3055 - 1 = -7.3055

$\Rightarrow{}$ The definition of the k.p Hamiltonians differs.

$M$ = 0.1956

$M_1$ = -0.1956 - 1 = -1.1956

$\Rightarrow{}$ The definition of the k.p Hamiltonians differs.

$N$ = 0.3813

$M_2$ = -0.3813 - 1 = -1.3813

$\Rightarrow{}$ The definition of the k.p Hamiltonians differs.

$R$ = 6.1227

$N_1$ = -0.3813 - 1 = -6.1227

$S$ = 0.4335

$M_3$ = -0.4335 - 1 = -1.4335

$\Rightarrow{}$ The definition of the k.p Hamiltonians differs

$T$ = 7.3308

$L_2$ = -7.3308 - 1 = -8.3308

$\Rightarrow{}$ The definition of the k.p Hamiltonians differs

$Q$ = 4.0200

$N_2$ = -4.0200

Conversion to “Luttinger” parameters:

$A_1$ = $L_2$ + 1 = -8.3308 + 1 = -7.3308

$\Rightarrow{}$ The definition of the k.p Hamiltonians differs.

$A_2$ = $M_3$ + 1 = -1.4335 + 1 = -0.4335

$\Rightarrow{}$ The definition of the k.p Hamiltonians differs.

$A_3$ = $M_2$ - $L_2$ = -0.3813 + 7.3308 = 6.9495

$A_4$ = 1/2 ($L_1$ + $M_1$ - 2 $M_3$) = -2.81705

$A_5$ = 1/2 ($L_1$ - $M_1$) = -3.05495

$\Rightarrow{}$ inconsistent to -3.06135

$A_5$ = 1/2 ($N_1$) = -3.06135

$\Rightarrow{}$ inconsistent to -3.05495

$A_6$ = $\sqrt{2}/2 N_2$ = -2.84256926

Cylindrical (axial) approximation:

[ZhangXia2006]:

\[L - M - R = 0\]

nextnano++:

\[L_1 - M_1 - N_1 = 0\]

\[\Rightarrow{} (A_2 + A_4 + A_5 - 1) - (A_2 + A_4 -A_5-1) - 2 A_5 = 0.\]

\[A_1 - A_2 = - A_3 = 2 A_4\]

\[A_3 + 4 A_5 = \sqrt{2} A_6\]

\[\Delta_2 = \Delta_3 = \frac{1}{3} \Delta_{so}\]

Last update: nn/nn/nnnn

[ZhangXia2006]	nextnano++
\(L\) = 6.3055	\(L_1\) = -6.3055 - 1 = -7.3055	\(\Rightarrow{}\) The definition of the k.p Hamiltonians differs.
\(M\) = 0.1956	\(M_1\) = -0.1956 - 1 = -1.1956	\(\Rightarrow{}\) The definition of the k.p Hamiltonians differs.
\(N\) = 0.3813	\(M_2\) = -0.3813 - 1 = -1.3813	\(\Rightarrow{}\) The definition of the k.p Hamiltonians differs.
\(R\) = 6.1227	\(N_1\) = -0.3813 - 1 = -6.1227
\(S\) = 0.4335	\(M_3\) = -0.4335 - 1 = -1.4335	\(\Rightarrow{}\) The definition of the k.p Hamiltonians differs
\(T\) = 7.3308	\(L_2\) = -7.3308 - 1 = -8.3308	\(\Rightarrow{}\) The definition of the k.p Hamiltonians differs
\(Q\) = 4.0200	\(N_2\) = -4.0200

\(A_1\) = \(L_2\) + 1 = -8.3308 + 1 = -7.3308	\(\Rightarrow{}\) The definition of the k.p Hamiltonians differs.
\(A_2\) = \(M_3\) + 1 = -1.4335 + 1 = -0.4335	\(\Rightarrow{}\) The definition of the k.p Hamiltonians differs.
\(A_3\) = \(M_2\) - \(L_2\) = -0.3813 + 7.3308 = 6.9495
\(A_4\) = 1/2 (\(L_1\) + \(M_1\) - 2 \(M_3\)) = -2.81705
\(A_5\) = 1/2 (\(L_1\) - \(M_1\)) = -3.05495	\(\Rightarrow{}\) inconsistent to -3.06135
\(A_5\) = 1/2 (\(N_1\)) = -3.06135	\(\Rightarrow{}\) inconsistent to -3.05495
\(A_6\) = \(\sqrt{2}/2 N_2\) = -2.84256926