Electron wave functions in a cylindrical well (2D Quantum Corral)

In this tutorial we demonstrate 2D simulation of a cilindrical quantum well. We will see the electron eigenstates and their degeneracy.

Input files used in this tutorial are the followings:

• 2DQuantumCorral_nn3.in / *_nnp.in

Structure

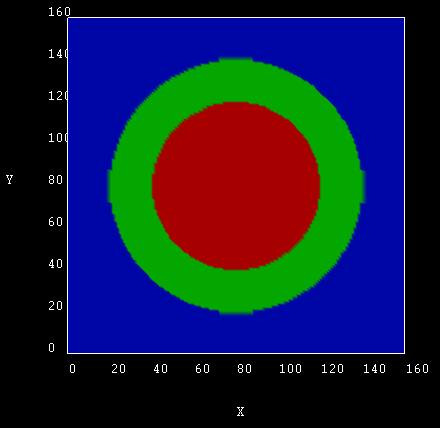
• A cylindrical InAs quantum well (diameter 80 nm) is surrounded by a cylindrical GaAs barrier (20 nm) which is surrounded by air. The whole sample is 160 nm x 160 nm.

• We assume infinite GaAs barriers. This can be achieved by a circular quantum cluster with Dirichlet boundary conditions, i.e. the wave function is forced to be zero in the GaAs barrier.

• The electron mass of InAs is assumed to be isotropic and parabolic (\(m_e = 0.026 m_0\)).

• Strain is not taken into account.

Simulation outcome

Electron wave functions

The size of the quantum cluster is a circle of diameter \(2a=80\) nm.

The following figures shows the square of the electron wave functions (i.e. \(\psi^2\)) of the corresponding eigenstates. They were calculated within the effective-mass approximation (single-band) on a rectangular finite-differences grid.

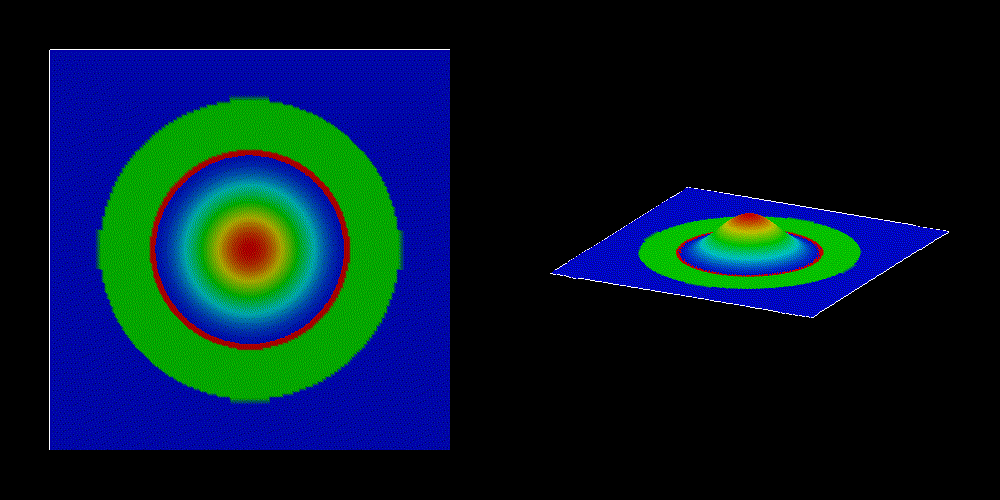
• 1st eigenstate, \((n,\ l)=(1,\ 0)\)

  

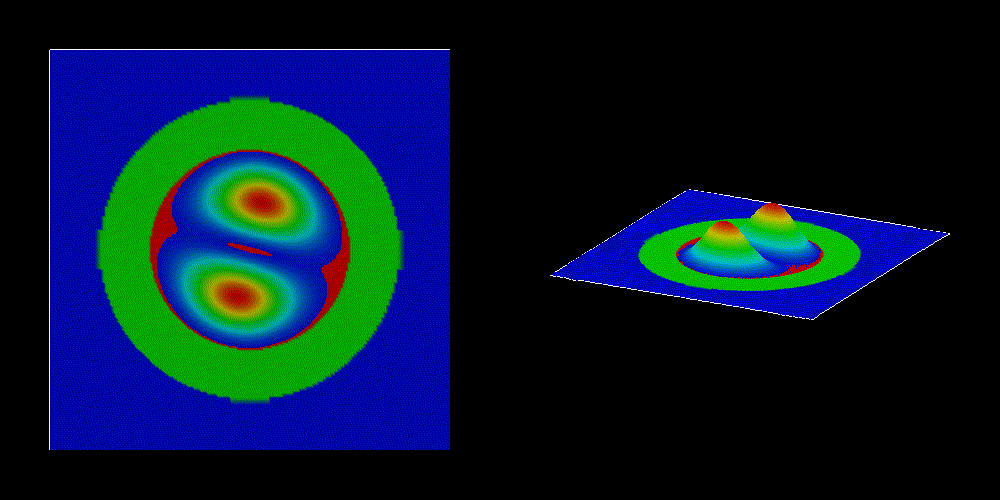
• 2nd eigenstate, \((n,\ l)=(1,\ 1)\)

  

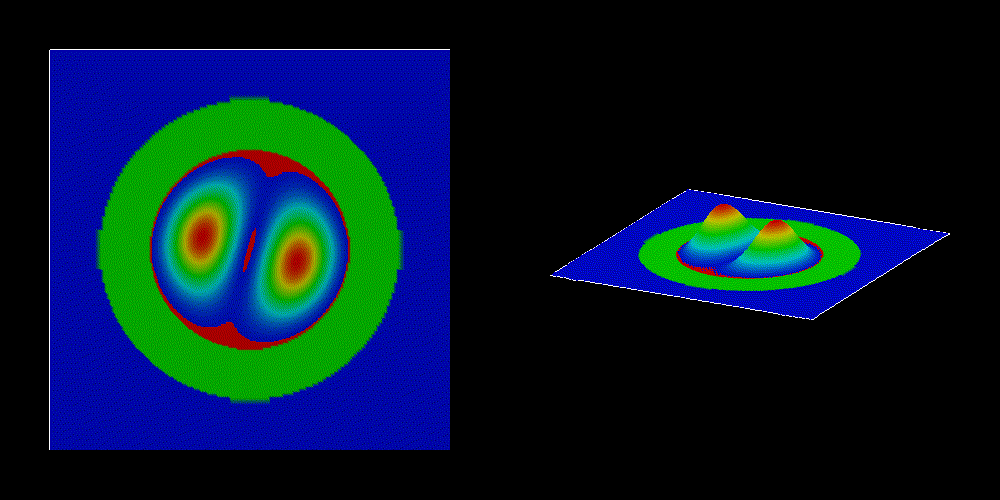
• 3rd eigenstate, \((n,\ l)=(1,-1)\)

  

• 4th eigenstate, \((n,\ l)=(1,\ 2)\)

  

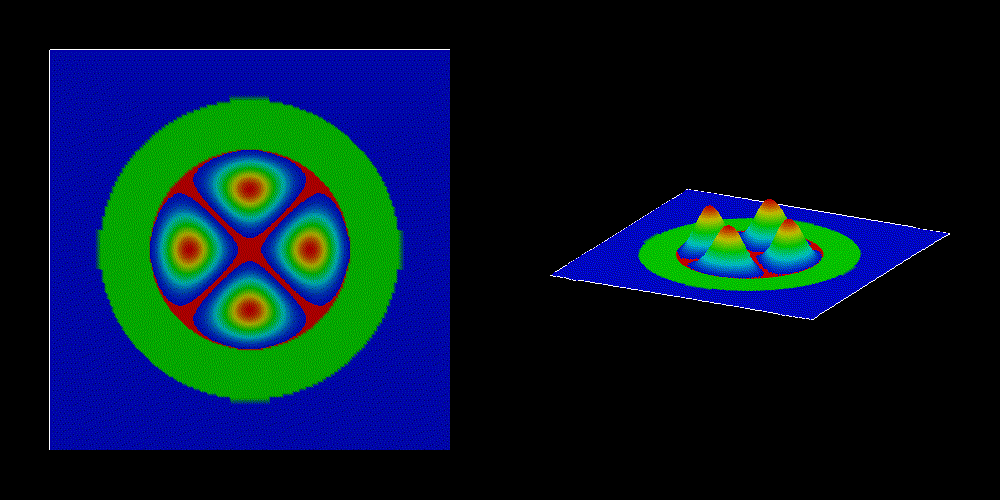
• 5th eigenstate, \((n,\ l)=(1,-2)\)

  

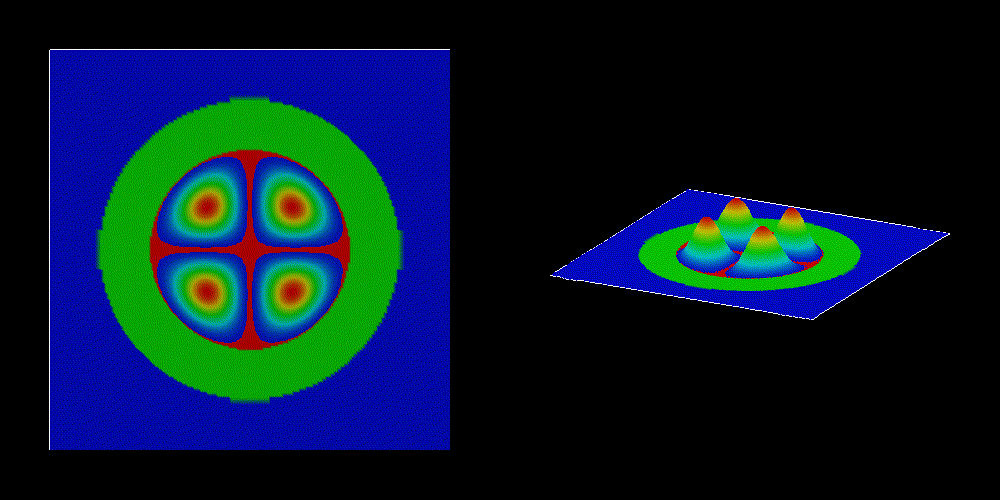
• 6th eigenstate, \((n,\ l)=(2,\ 0)\)

  

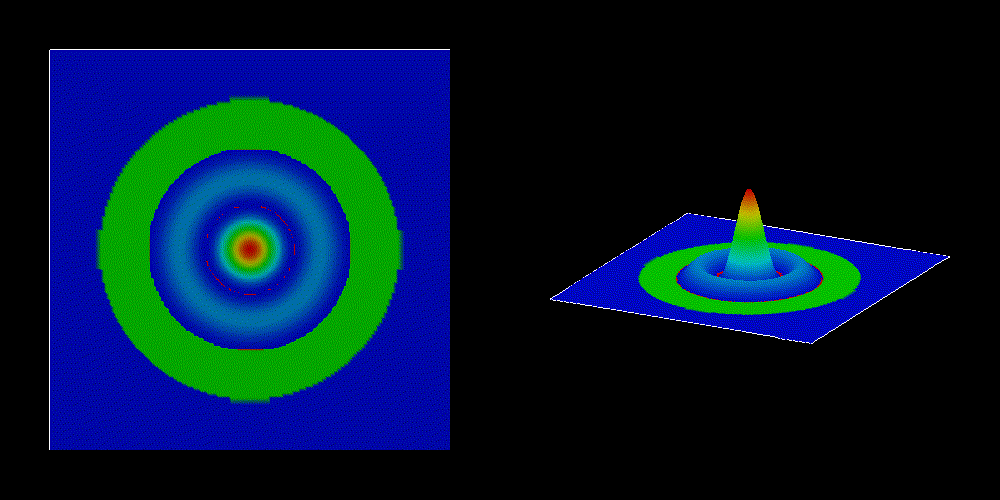
• 15th eigenstate, \((n,\ l)=(3,\ 0)\)

  

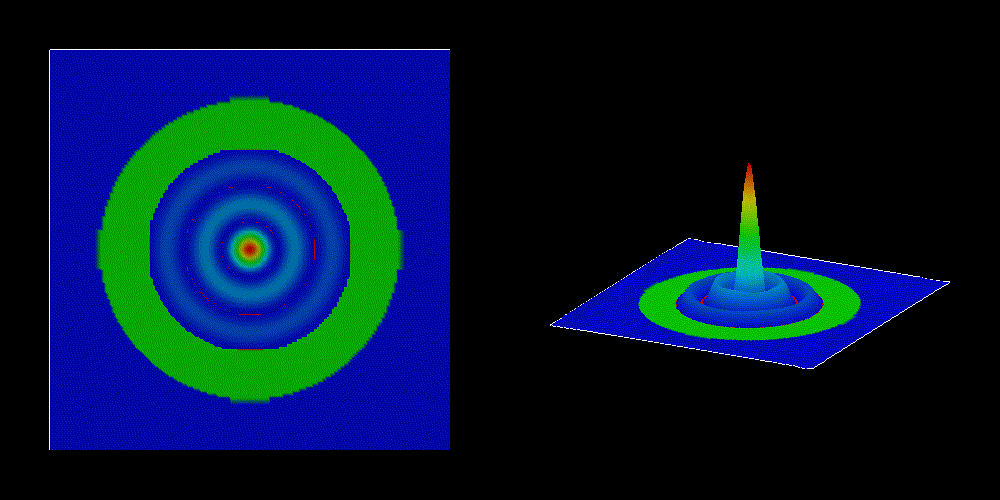
• 20th eigenstate, \((n,\ l)=(1,\ 6)\)

  

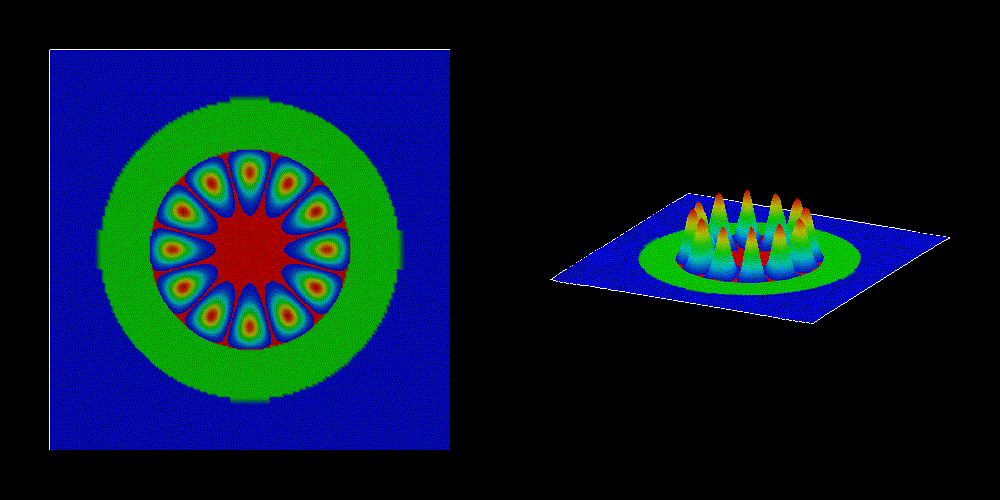
• 22th eigenstate, \((n,\ l)=(3,\ 1)\)

  

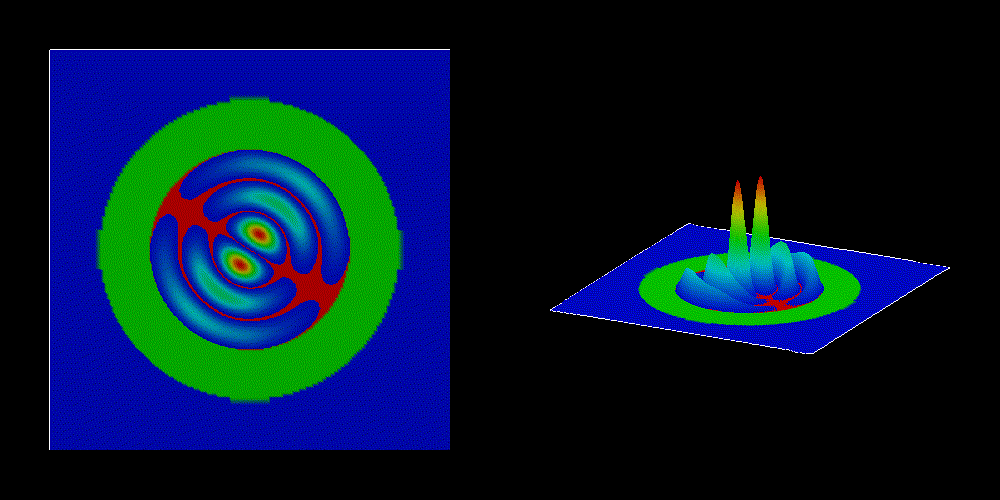
The parameters of the quantum corral are the followings:

• radius: \(a = 40\) nm

• \(m_e = 0.026 m_0\)

• \(V(r) = 0\) for \(r < a\)

• \(V(r) = \infty\) for \(r > a\)

The analytical solution of the eigenstates of this quantum well is:

(2.4.45)\[\psi_{n,l}(r,\theta) \propto J_{l}\left(\frac{j_{l,n}r}{a}\right)\left[A\cos(l\theta)+B\sin(l\theta)\right]\]

where

• \(J_{l}(x)\) is the Bessel function of the first kind (We cite them for \(l=0,1,2\) below.)

• \(j_{l,n}\) is its zero point i.e. \(J_l(j_{l,n})=0\) and \(n=1,2,...\)

• \(A,B\) are constant

• \(l=0, \pm 1, \pm 2, ...\)

The corresponding eigenenergies are: \(E_{nl} = \frac{\hbar^2j_{l,n}^2}{2m_e a^2}\)

The Quantum number \(n\) comes from the boundary condition \(\psi(a, \theta)=0\). The requirement that \(\psi\) has the same value at \(\theta=0\) and \(2\pi\) leads to the quantum number \(l\). In the above figures of the eigenstates, we can know them through the following relations:

• (the number of zero points in the radial direction) \(=n\)

• (the number of zero points in the circumferential direction)/2 \(=|l|\)

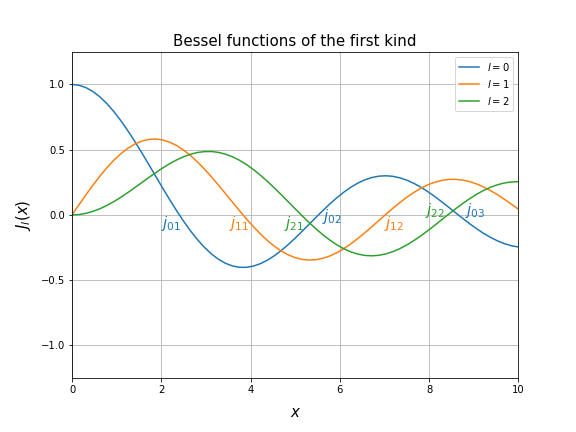
Figure 2.4.164 Bessel functions of the first kind for \(l=0,1,2\) generated by scipy.

Energy spectrum

The following figure shows the energy spectrum of the quantum corral. (The zero of energy corresponds to the InAs conduction band edge.)

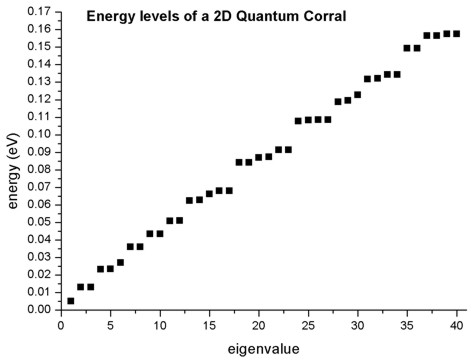
The two-fold degeneracies of the states

• (2, 3), (4, 5), (7, 8), (9, 10), (11, 12), (13, 14), (16, 17), (18, 19), (20, 21), (22, 23), (24, 25), (26, 27), (28, 29), (31, 32), (33, 34), (35, 36), (37, 38), (39, 40)

correponds to \(|l|\ge1\). On the other hand, the non-degenerate energy eigenvalues corresponds to \(l=0\)

The analytical energy values are: \(E_{nl} = \frac{\hbar^2j_{l,n}^2}{2m_e a^2}\).

There is a formula to approximate \(j_{l,n}\): \(j_{l,n} = ( n + \frac{1}{2} | l | - \frac{1}{4} ) \pi\) which is accurate as \(n \rightarrow \infty\).

Here we describe the comparison between the analytical values, approximate values, nextnano++ results and nextnano³ results.

	\([n,l]\)	\(j_{l,n}\)	\(j_{l,n}\) (approx.)	\(E_{n,l}\) [eV]	\(E_{n,l}\) [eV] (approx.)	\(E_{n,l}\) [eV] (nextnano++)	\(E_{n,l}\) [eV] (nextnano³)
1st	[1, 0]	2.405	0.75\(\pi\simeq\)2.356	0.00530	0.00508	0.00510	0.00511
2nd	[1, 1]	3.832	1.25\(\pi\simeq\)3.926	0.01345	0.01412	0.01294	0.01298
3rd	[1,-1]	3.832	1.25\(\pi\simeq\)3.926	0.01345	0.01412	0.01294	0.01298
4th	[1, 2]	5.136	1.75\(\pi\simeq\)5.497	0.02416	0.02768	0.02320	0.02325
5th	[1,-2]	5.136	1.75\(\pi\simeq\)5.497	0.02416	0.02768	0.02329	0.02325
6th	[2, 0]	5.520	1.75\(\pi\simeq\)5.497	0.02791	0.02767	0.02685	0.02693
7th	[2, 1]	7.016	2.25\(\pi\simeq\)7.067	0.04508	0.04574	0.03584	0.03597

Further details about the analytical solution of the cylindrical quantum well with infinite barriers can be found in:

The Physics of Low-Dimensional Semiconductors - An Introduction

John H. Davies

Cambridge University Press (1998)

Last update: nn/nn/nnnn